ما هو افضل اليانصيب

القاعدة 4. ابدأ في الوقت المحدد

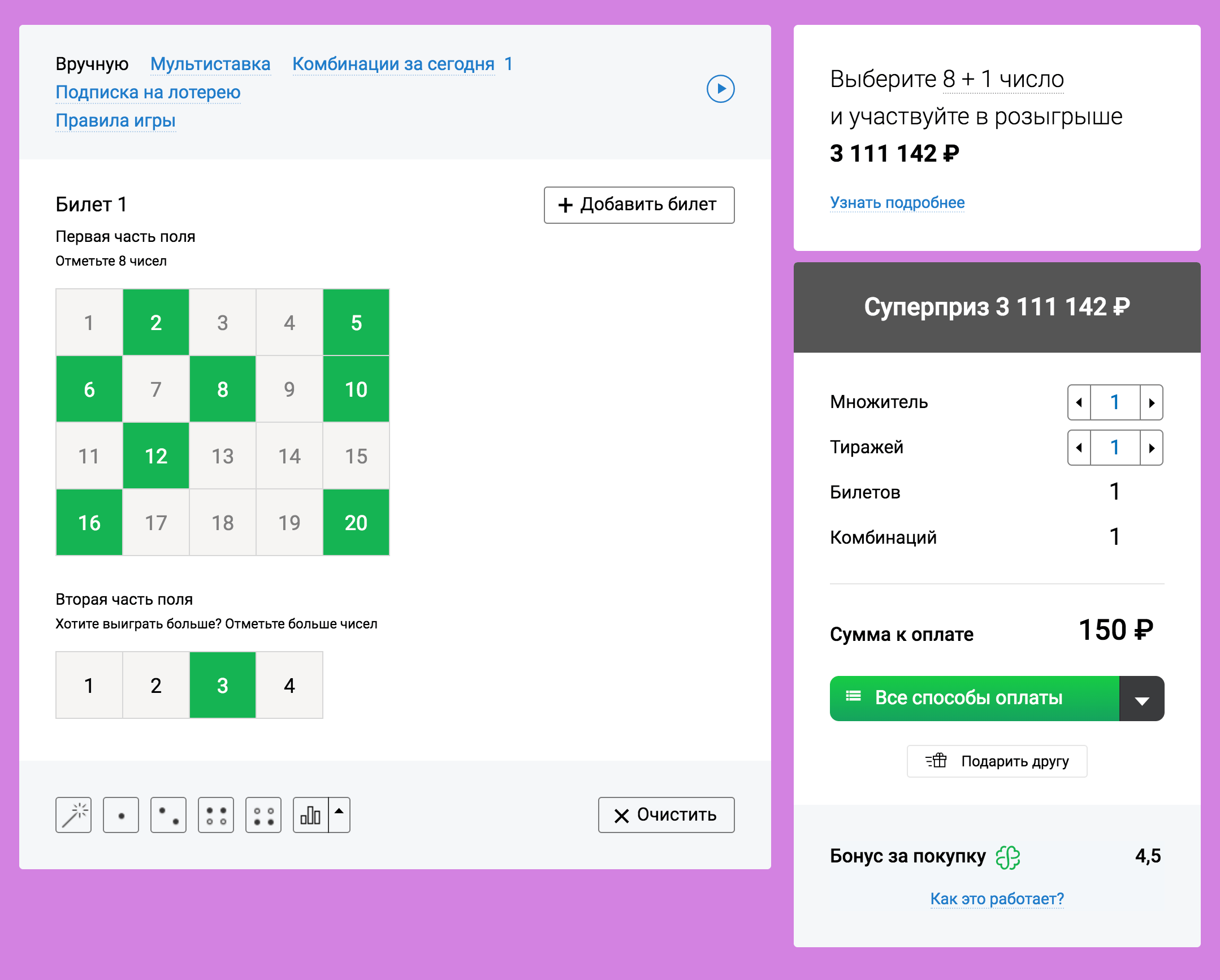
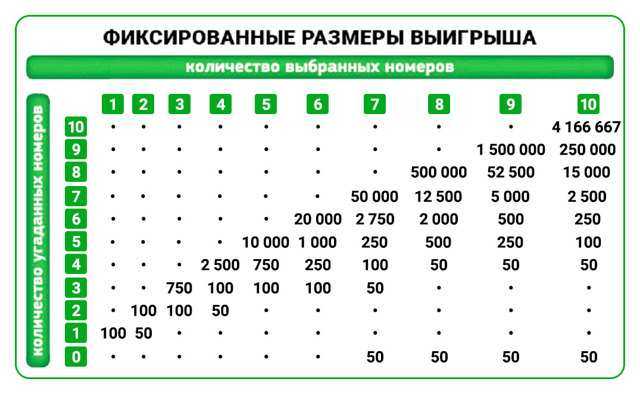
تذكرة يانصيب PowerBall, على فكرة, يستحق 2 دولار. لحساب الفوائد, والتي من شأنها سداد ثمن شراء التذكرة, нужно умножить цену билета на 292 201 338.

المزيد عن العمليات الحسابية. هذه إشارة إلى النقطة الأولى., حيث تقول, أن فائدة الحل تساوي قيمته, مضروبة في الاحتمال. إذا كان لدينا حدث مع احتمال 1 / X والقيمة N, ثم ستكون الفائدة N / X. Мы тратим 2 доллара и можем подсчитать, ما مقدار المكاسب التي ستدفع مقابل شراء تذكرة:

• 2 = N ÷ X.
• N = 2 × X, а X тут как раз равен 292 201 338, كما يتضح من الحسابات من الجزء السابق.

تحتاج أيضًا إلى مراعاة الضرائب (اكتشف, ما هي النسبة المئوية للمبلغ المعلن الذي سيذهب بالفعل إلى الفائز, عادة ما يكون حول 70%). То есть джекпот должен составлять как минимум 850 مليون دولار, وهذا يحدث في هذا اليانصيب. كيف ذلك, قلت في البداية, أن الكسب في مثل هذا الضرب لا يكون دائمًا لصالح اللاعب?

الحقيقة, ماذا لو لم يتم سحب الجائزة الكبرى, ثم يذهب في المرة القادمة, وهذا هو سبب تراكم المال لبعض الوقت, وتستمر مبيعات التذاكر.

لكن من المستحيل معرفة ذلك مسبقًا. ومع ذلك ، يمكنك البدء في شراء التذاكر, بمجرد أن يتجاوز حجم الجائزة الكبرى المبلغ المذكور. في مثل هذه الحالة ، من الناحية الحسابية ، ستكون اللعبة مفيدة.

لا يزال بإمكانك أن تفهم, أيهما أكثر ربحية: شراء العديد من التذاكر للعبة واحدة أو شراء تذكرة واحدة للعديد من الألعاب? لنفكر.

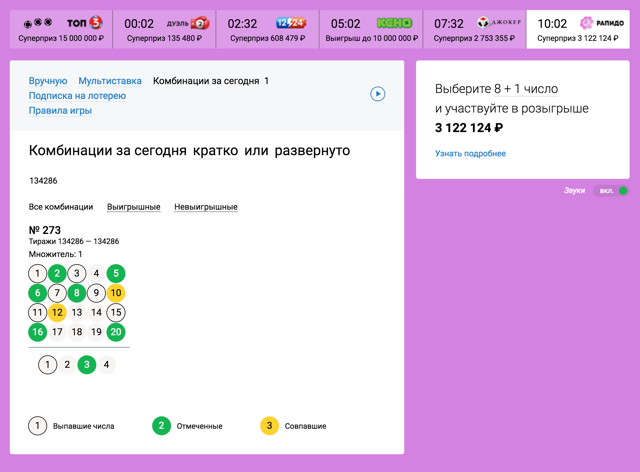
في نظرية الاحتمالات يوجد مفهوم للأحداث غير ذات الصلة. هذا يعني, أن نتيجة أحد الأحداث لا تؤثر على نتيجة حدث آخر. فمثلا, إذا رميت نردتين, ثم لا ترتبط الأرقام المتساقطة عليها: من حيث العشوائية, لا يؤثر الموت الواحد على سلوك الآخر. ولكن إذا قمت بسحب ورقتين من على سطح السفينة, ثم ترتبط هذه الأحداث, لأن البطاقة الأولى تعتمد على, ما هي البطاقات التي ستبقى في المجموعة.

يُطلق على أحد المفاهيم الخاطئة الشائعة حول هذا الأمر خطأ اللاعب.. ينشأ من فكرة الشخص البديهية عن الترابط بين الأحداث غير ذات الصلة.

العودة إلى اليانصيب: الألعاب المختلفة هي أحداث غير ذات صلة, لأنه تم إعادة اختيار تسلسل الكرات. لذا فإن فرص الفوز بأي يانصيب معينة لا تعتمد على ما إذا كان, كم مرة لعبت فيها من قبل. من الصعب جدًا قبوله بشكل حدسي., لأن الإنسان في كل مرة, شراء تذكرة, يعتقد: "حسنًا ، أنت الآن محظوظ, كم من الوقت, لقد كنت ألعب كثيرًا من الوقت!" لكن لا, نظرية الاحتمالية شيء بلا قلب.

لكن شراء تذاكر متعددة للعبة واحدة يزيد من فرصك بشكل متناسب, لأن التذاكر داخل لعبة واحدة مرتبطة: إذا فاز أحد, يعني, آخر (مع تركيبة أخرى) بالتأكيد لن يفوز. Покупка 10 билетов увеличивает шансы в 10 زمن, إذا كانت جميع المجموعات الموجودة على التذاكر مختلفة (في الواقع ، دائمًا ما يكون كذلك). بعبارات أخرى, если у вас есть деньги на 10 تذاكر, من الأفضل شرائها للعبة واحدة, чем покупать по билету на 10 ألعاب.

إذا كنت تأخذ تذكرة من راتبك مرة واحدة في الشهر من أجل, ثم, المحتمل أن, عملية اللعب تهمك. Математически выгоднее скопить эти деньги и в конце года купить сразу 12 تذاكر, برغم من, بالطبع, سوف يُنظر إلى الخسارة في مثل هذه الحالة على أنها أكثر تدميراً.

القاعدة 1. تقييم المخاطر

ليس سرا لشخص مستنير حديث, أن الكازينوهات ومؤسسات المقامرة المختلفة تحسب جميع ألعابها على أنها, أن تكون الفائز دائمًا وتحقق ربحًا. يتم ذلك بكل بساطة: يحتاج الشخص إلى إعادة المكاسب, الذي يرتبط برهانه التنازلي مقارنة بفرصه في الفوز.

لا توجد استثناءات, ما لم يرغب شخص ما على وجه التحديد في منحك المال. ضع هذه القاعدة البسيطة في الاعتبار, أن ننظر دائمًا إلى الوضع برصانة.

تقيم نظرية اللعبة أي استراتيجية بنفس الطريقة: يتضاعف احتمال الفوز بحجمه. تحدث تقريبا, تحسب الرياضيات, что гарантированно получить 1 000 рублей — это как получить 2 000 рублей с 50-процентным шансом. يمنحك هذا المبدأ القدرة على مقارنة الألعاب المختلفة تقريبًا مع بعضها البعض.. ما الأفضل: миллион долларов с шансом 1/100 000 أو 50 долларов с шансом 1/4? يبدو الأمر بديهيًا, أن الجملة الأولى أكثر إثارة للاهتمام, لكن الأخير أكثر فائدة من الناحية الرياضية.

إذا بقيت في إطار الرياضيات وحدك, يمكن حسابها: من المستحيل الفوز في الكازينو, لأن أي استراتيجية يتم اختيارها تؤدي إلى, أن ناتج احتمالية الفوز وحجم الدفع للاعب دائمًا أقل, وهو ما فعله بالفعل.

وأيضًا لأن, هذا المال غير خطي بالنسبة لنا: формально получить 1 рубль прямо сейчас — это как получить миллион рублей с шансом 1/1 000 000, لكن في الواقع ، لن يؤثر فقدان الروبل على حالتنا بأي شكل من الأشكال, لن يتغير شيء في الحياة, لكن الحصول على مليون هو حدث خطير للغاية.