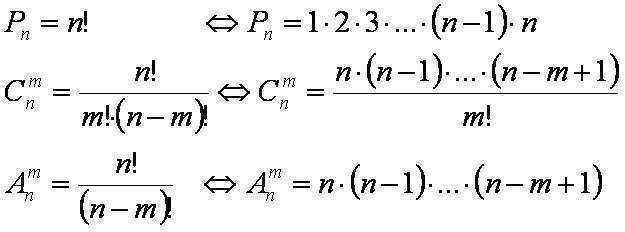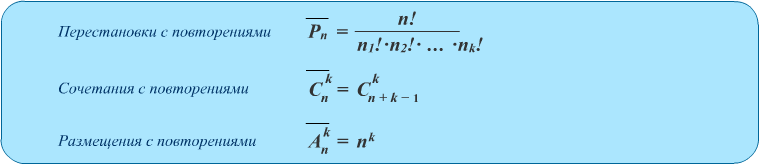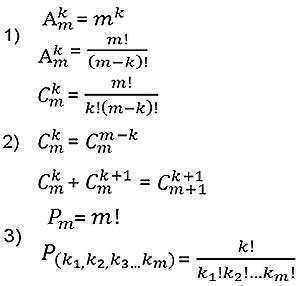Kombinationselementer

Pengens magi i numerologi

Hvert nummer har sin egen energi og påvirker en persons liv på en bestemt måde.. Numerologi af penge hjælper med at bestemme betydningen af ​​et tal, finde ud af den personlige kode for penge og velstand. Fiskal kode beregnes ved hjælp af fødselsdato. Så skal du se udskriften. Du skal også vide, hvordan du bruger din formuekode korrekt.

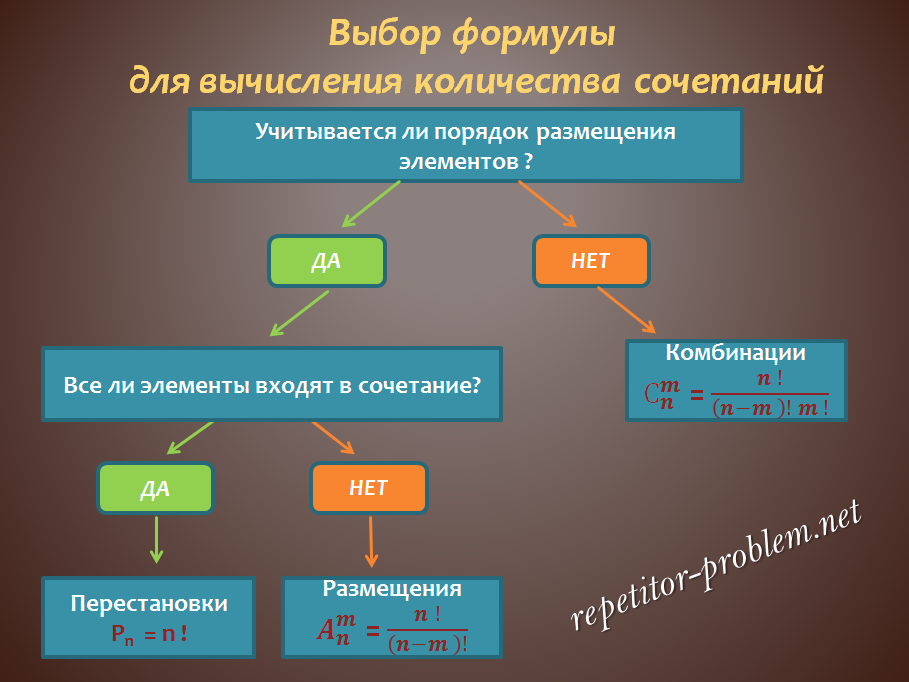
Det vigtigste er at beregne den finansielle kode korrekt

Udover, hvad er antallet af velstand, der er også tal, ikke bringe overflod til en persons liv. De skal undgås. At tiltrække økonomisk strøm, har brug for at gøre dig bekendt med, hvad står hvert nummer for:

1. Nul og en. Numerologer tror, at disse tal og koder er negative for monetær energi, de bringer ikke held og lykke. Derfor bør du undgå besparelser., indskud med beløb, hvor disse tal er til stede, fordi de vil bremse pengestrømmen og ikke medføre velstand og succes.
2. Par. Dette er en ulykkelig figur. Hun bringer ikke velstand og succes. Det anbefales ikke at bruge pengesedler fra denne betegnelse til opsparing, ikke bære dem i din tegnebog.
3. Trekløver. Er økonomisk gunstig, med sin hjælp kan en person vinde lotteriet, finde yderligere indtægtskilder. Men numerologer anbefaler ikke at akkumulere midler., hvis sum er 300, 3000, 30000. Denne figur har brug for konstant bevægelse, hun har brug for energi, ikke fred. Det bedste er at købe en lotteri til et sådant beløb eller investere det i din egen virksomhed..
4. De fire i den personlige kode er et symbol på stabilitet, pålidelighed. Ideel til besparelser, opsparing, investering er mængden af ​​regninger 400, 4000, 40000. På denne måde, velstand øges.
5. Fem er en meget vigtig numerisk rigdomskode inden for numerologi. Regninger med dette nummer er magneter med rigtige penge.. De kan lånes, bruge på rejser, ophobe, bruge det, som du vil.
6. En sådan finansiel kode kan tiltrække visse økonomiske begrænsninger. Med denne figur lærer folk at spare, kontrollere dine udgifter. Beløb 600, 6000 er et symbol på stabilitet og sikkerhed. Numerologer anbefaler ikke at investere sådanne beløb.
7. Syv er kode, uheldig, det kan ikke bruges til opbevaring, investeringer, opsparing, lån og andre finansielle transaktioner, som er forbundet med risiko.
8. Otte er en stærk velstandskode inden for numerologi, han betragtes som meget succesrig. Indskud på beløb 800, 8000, 80000 er meget succesrige, de tiltrækker penge, som en magnet.
9. Ni er et symbol på spiritualitet og indre udvikling. At skaffe penge med det sker ikke, men der vil heller ikke være noget tab. Det anbefales at bruge summer med en ni på selvstudium, uddannelse

At bruge tal korrekt, har brug for at vide, hvordan man beregner formuekode. Dernæst skal du finde ud af reglerne for brug af en sådan kombination.. Bliver jeg rig, afhænger ikke kun af den kode, der er opnået som et resultat af beregningen, men også ud fra det, hvor korrekt det skal bruges.

referenceoplysninger

DokumenterRapporteraf nævner Dokumentbase VærdipapirerBestemmelserFinansielle dokumenterOpløsningerRubrikator efter emne Finans Byer i Den Russiske Føderation regioner efter nøjagtige datoerBetingelserVidenskabelig terminologi Finansiel økonomiskTidDatoer 2015 2016 Dokumenter i den finansielle sektor i investeringen

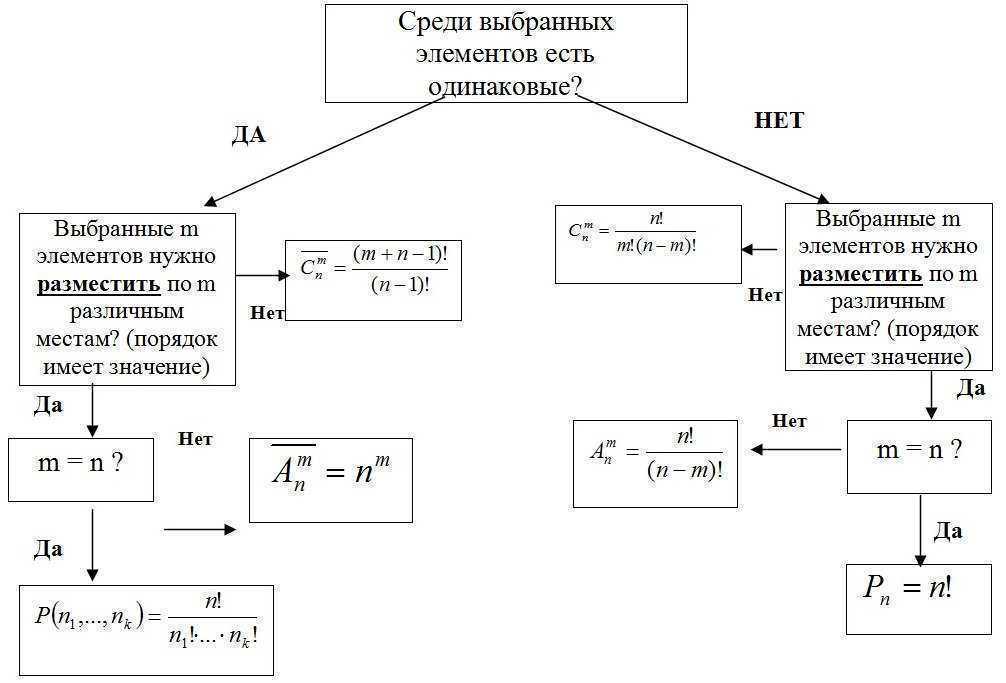
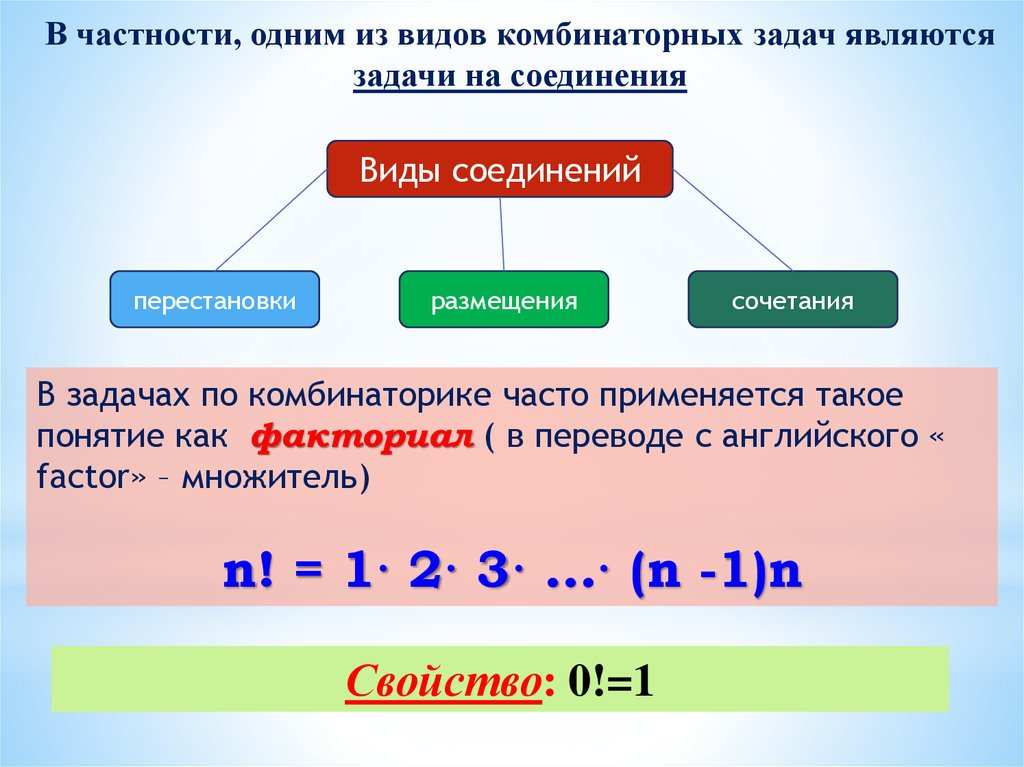
Kombinationer uden gentagelser

En opgave: Find alle mulige kombinationer uden gentagelser fra mange elementer {1,2,3} ved 2.
Følgende kombinationer findes:1: 1 22: 1 33: 2 3
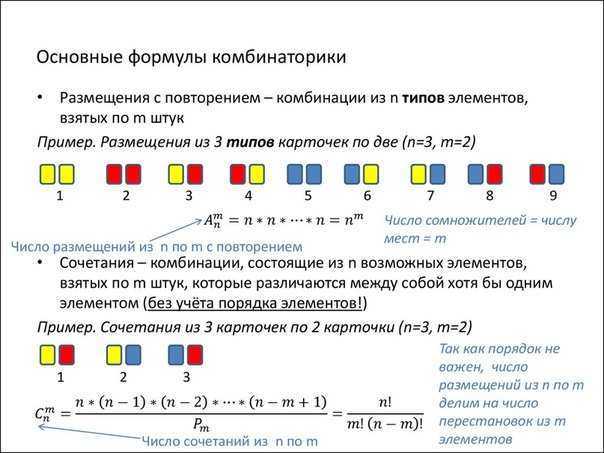
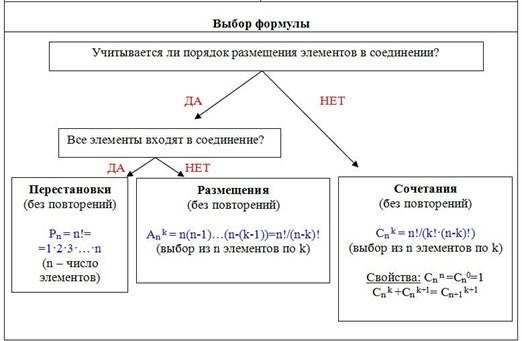
Antallet af mulige kombinationer uden gentagelser af N-elementer ved M kan bestemmes af formlen (N≥M):

det i M! gange mindre end det tilsvarende antal placeringer uden gentagelser (da kombinationer uden gentagelser ikke afhænger af elementernes rækkefølge).
Overvej problemet med at få alle kombinationer til tal 1 ... N af M. Implementering i C ++

12345678910111213141516171819202122232425262728293031323334353637383940414243

#omfatte <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int k = m; til (int i = k – 1; jeg >= 0; –jeg) hvis (-en < n – k + jeg + 1) { ++-en; til (int j = i + 1; j < k; ++j) a = a + 1; return true; } returner falsk;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; til (int i = 0; jeg < n; i++) cout << -en << ” “; cout << endl;}int main() { int n, m, *-en; cout << “N = “; cin >> n; cout << “M = “; cin >> m; a = new int; til (int i = 0; jeg < n; i++) a = i + 1; Print(-en, m); hvis (n >= m) { mens (Næste sæt(-en, n, m)) Print(-en, m); } cin.get(); cin.get(); Vend tilbage 0;}

Результат выполнения

Engelsk numerologi: koncept og essens

Den ældste viden, som hjælper med at forklare, fortolke det, hvad engle vil fortælle mennesket, kaldet engle numerologi.

Minde om, at numerologi studerer talvibrationer, cifre, deres indflydelse på mennesker og deres livsprocesser. En anden engelsk matematiker, astrolog John Dee i det 16. århundrede skrev et værk om tal, som han betragtede som det universelle englesprog til kommunikation med mennesker.

Grundlæggeren af ​​den relativt unge undervisning i Angelic Numerology er Doreen Verche. Klarsynt fra Amerika, psykolog og filosof, forfatter af mange bøger. Hun dedikerede sine værker til de højeste væsener, inklusive guder, engle, hellige. I mange år har hun forsket på uforklarlige fænomener.. Men det var det værd. Hun skabte instrumentet, som kan hjælpe dig med at fortolke budskaber fra dine hjælpere fra himlen. Ifølge Doreen Verce, vi modtager regelmæssigt tegn fra engle, der advarer om farer, foreslå løsninger på problemer i en persons liv.

Engle taler med mand efter tal, bogstaver, tegn. Doreen Verces værker taler om spor fra usynlige brugere, som er kodet i gentagne cifre eller kombinationer deraf. Nemlig:

• på bilskilt;
• på uret;
• i kagen, lejlighed, kontor nummerering;
• i fødselsdatoer;
• i billetformularer, som i transport, og offentlige faciliteter mv..

I alle sådanne kombinationer, tal skjuler data, der kan foretage tilpasninger af fremtidens mennesker. Doreen Verce har forsket meget i emnet, dedikeret til numerologiske beregninger efter fødselsdato. Sådanne beregninger hjælper med at identificere børn., der har unikke evner fra fødslen, og ikke kun.

Antal matches, kombinationer, som vi ofte ikke bemærker

Men det er værd at være opmærksom på, fordi et sådant fænomen kan være en vigtig advarsel. Når alt kommer til alt, sender engle os ikke sådan et tegn for ingenting

Kombinationer med gentagelser

Kombinationer med gentagelser er sæt M-elementer, hvor hvert element i sættet N kan deltage flere gange. I dette tilfælde pålægges der ingen begrænsninger for forholdet mellem værdierne M og N, og det samlede antal kombinationer med gentagelser er

Et eksempel på et sådant problem er valget af M-postkort fra N på alle mulige måder.

For at generere kombinationer med gentagelser bruger vi løsningen til at generere placeringer med gentagelser., C ++ implementering

1234567891011121314151617181920212223242526272829303132333435363738394041

#omfatte <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int j = m – 1; mens (a == n && j >= 0) j–; hvis (j < 0) returner falsk; hvis (-en >= n) j–; a++; hvis (j == m – 1) return true; til (int k = j + 1; k < m; k++) a = a; return true;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; til (int i = 0; jeg < n; i++) cout << -en << ” “; cout << endl;}int main() { int n, m, *-en; cout << “N = “; cin >> n; cout << “M = “; cin >> m; int h = n > m ? n : m; // размер массива а выбирается как max(n,m) a = new int; til (int i = 0; jeg < h; i++) a = 1; Print(-en, m); mens (Næste sæt(-en, n, m)) Print(-en, m); cin.get(); cin.get(); Vend tilbage 0;}

Resultatet af ovenstående algoritme:

Algoritmisering

Grundformel for kombinatorik

Lad der være k grupper af elementer, og den i-gruppe består af n_jeg elementer.
Vælg et element fra hver gruppe. Derefter det samlede antal N måder,
med hvilket et sådant valg kan træffes, er defineret af forholdet N = n₁*n₂*n₃*…*n_k.

Eksempel 1. Lad os forklare denne regel på en enkel måde
eksempel. Lad der være to grupper af elementer, og den første gruppe består af
n₁ elementer, og det andet – af n₂ elementer. hvor mange
forskellige par af elementer kan være sammensat af disse to grupper, på denne måde,
så der er et element i et par fra hver gruppe? Lad os indrømme, Vi tog
det første element fra den første gruppe og, uden at ændre det, gik over alt muligt
par, kun at ændre elementer fra den anden gruppe. Sådanne par til dette element
kan være n₂. Så tager vi det andet element fra den første gruppe
og komponer også alle mulige par til det. Der vil også være n sådanne par₂.
Da den første gruppe kun indeholder n₁ element, alt muligt
valgmulighederne er n₁*n₂.Eksempel 2. hvor mange
trecifrede lige tal kan bestå af cifre 0, 1, 2, 3, 4, 5, 6, hvis
numre kan gentages?Afgørelse: n₁= 6
(fordi. som det første ciffer kan du tage ethvert ciffer fra 1, 2, 3, 4, 5, 6), n₂= 7
(fordi. som det andet ciffer kan du tage ethvert ciffer fra 0, 1, 2, 3, 4, 5,
6), n₃= 4 (fordi. som det tredje ciffer kan du tage ethvert ciffer fra 0, 2, 4,
6).

så, N = n₁*n₂*n₃= 6 * 7 * 4 = 168.

I det tilfælde, når alle grupper har det samme antal elementer, dvs.. n₁= n₂=…n_k= n
det kunne overvejes, at hvert valg er taget fra den samme gruppe, i øvrigt
elementet efter valg vender tilbage til gruppen igen. Så antallet af alle måder
valget er nk. Denne type valg i kombinatorik kaldes selektion med retur.

Eksempel 3. Hvor mange er alle firecifrede tal
kan bestå af tal 1, 5, 6, 7, 8?Afgørelse. For hver rang
et firecifret tal er der fem muligheder, betyder N = 5 * 5 * 5 * 5 = 54 = 625.

Overvej sættet, bestående af n elementer. det
et sæt i kombinatorik kaldes generelt
samlet.

Erhverv og økonomi

BankerRigdom og velfærdKorruption(Forbrydelse)MarketingLedelseInvesteringerSikkerhedLedelseOffentlige aktieselskaberProjekterDokumenterSikkerhed – kontrollere værdipapirer – Værdiansættelsesobligationer Gæld Valuta Fast ejendom(Leje)ErhvervJobsHandlingTjenesterFinansInsuranceBudgetFinansielle tjenester

Hvad skal man gøre med den mantriske kode efter at have gennemført ritualet

Efter, hvordan numeriske værdier blev aflæst under 77 dage, de skal sigtes for 4 elementer til videre arbejde.

For at gøre dette skal du udføre enkle manipulationer.:

1. Aktivér koden med Jordens energi. En lille jordkrukke er velegnet til ritualet.. Du skal også bruge blomsterfrø. Disse skal være nøjagtigt frøene., ikke planternes skud og knolde. Efter forberedelse af de krævede attributter, mantraet skal skrives på et stykke blankt papir og nedgraves i jorden, siger ordene tre gange - ”Jorden er fuld af rigdom, du er nu min drøm ”. Dernæst placeres et blomsterfrø i potten.
2. Efter jordens element er mantraet ladet med vandets energi. Dette ritual består i vanding af frøet, som ledsages af ordene ”Vand og jord, genoplive frøene ”. Som i det foregående tilfælde, afgive en erklæring 3 gange.
3. Dernæst kommer turen til elementerne i Air. Gryden med den fremtidige plante skal bringes til et åbent vindue og sagde: "Du, Luft, jeg behøver, som lys, og giv min drøm Dawn ". Det skal gentages indeni 3 dage.
4. Når et frøspire vises, det er tid til elementerne i ild. Et nyt tændt lys er nødvendigt for at vække mantraet. Det skal placeres ved siden af ​​planten og, koncentrere sig, sig tre gange: ”Det brænder, Ild, stearinlys - udbrændt, og ødelægge fattigdom. Lad spiren vokse, hvad skjuler pengene sig. Og jeg vil blomstre med ham, tiltrække rigdom i penge ".

Efter disse trin begynder valutakoden at fungere. Det tilrådes ikke at smide gryden sammen med spire og mantra, fortsætter den sædvanlige pleje af planten.

Udover, for at forbedre effekten af ​​den mantriske kode, Du kan anvende billedet af tal på et ark pap med grønt og rødt blæk. En sådan pengetalisman skal konstant bæres med dig..

Magien ved velkendte ting

Vores tilfældige tilfældige talgenerator online.

Vores randomiseringsgenerator kræver ikke download af den til din personlige pc. Alt sker i online nummergenerator-tilstand. Angiv bare disse parametre, som: række numre online, hvor numrene vil blive tilfældigt valgt. Angiv også antallet af numre, som vælges.
For eksempel, у Вас есть группа Вконтакте. В группе вы разыгрываете 5 præmier, blandt deltagerne, hvem vil genindgive posten. Brug af en dedikeret app, vi fik en liste over deltagere. Hver er tildelt et løbenummer for numre online.

Gå nu til vores online generator og specificer rækkevidden (antal deltagere). for eksempel, spørge, hvilke numre online har brug for 5, siden vi har gjort det 5 præmier. Теперь жмем кнопку генерации. Så får vi 5 tilfældige tal online, spænder fra 1 til 112 inklusive. Genereret 5 numre online svarer til serienummeret på fem deltagere, der blev vinderne af tegningen. Alt er simpelt og praktisk.

Et andet plus ved tilfældig talgenerator er, at alle numre online gives tilfældigt. Det vil sige at påvirke ham, eller beregne, hvilket antal bliver næste, synes ikke muligt. Hvad generatoren gør kan siges, Ærlig og pålidelig, og administrationen, der giver præmier væk ved hjælp af vores gratis generator, ærlig og anstændig over for deltagerne i konkurrencen. Og hvis du er i tvivl om en løsning, så kan du bruge vores ja eller nej svar generator.

Sådan beregnes din formuekode

Der er gode og dårlige kombinationer

Numerologi og penge er tæt forbundet. Der er talkombinationer, velstandsskabende, men der er mislykkede kombinationer. Hvis du anvender dem korrekt, succes og held vil være på din side. Det er let at beregne koden. For at gøre dette skal du udføre følgende beregninger:

• skriv dit nummer på et blankt stykke papir, måned og fødselsår (f.eks, 31.10.1987);
• at beregne succesværdien, de to første cifre skal tilføjes, dvs., specifik fødselsdato (f.eks, 31 - 3 + 1 = 4). Dette nummer vil være det første i kombinationen;
• at beregne kombinationens andet tegn, det er nødvendigt at beregne månedens værdi (f.eks, oktober, 10 måned - 1 + 0 = 1);
• nu skal du beregne mængden af ​​fødselsåret (f.eks, 1987 - 1 + 9 + 8 + 7 = 25, 2+5= 7);
• i slutningen skal du personligt beregne det sidste tegn i kombinationen, for dette opsummeres alle tre tidligere modtagne numre (f.eks, 4+1+7= 12, 1+2= 3, i dette tilfælde er pengekombinationen 4173). Den resulterende kombination er en personlig kode for en person..

Ud over den personlige kode, der er universelle værdier, at alle kan ansøge, som en millionær, og med mellemindkomst. Dette er en digital maskot, som er afbildet i form af fire otter af samme størrelse. Denne kombination er meget stærk, betyder monetær succes og stabilitet.

Du kan også beregne derefter, vil jeg være rig, ved navn. Til dette tages en tabel over korrespondance mellem bogstaver og tal. For eksempel, Marina, som blev født 5 numre. I dette tilfælde tages kun fødselsdagen:

M-5, A-1, R-9, I-1, N-6, A-1. 5+1+9+1+6+1= 23, 2+3= 5. Dernæst tilføj fødselsdatoen - 5 + 5 = 10, 1+0= 1 - en og er koden for held og penge for en bestemt person. Men kan han få succes, afhænger af, hvor godt det bruges.

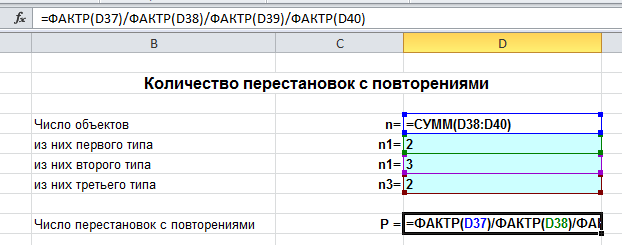
Permutationer af n elementer

Definition 3. Permutation
af n elementer
ethvert bestilt sæt kaldes
disse elementer.

Eksempel 7a. Alle slags permutationer
skarer, bestående af tre elementer {1, 2, 3} er: (1, 2, 3), (1, 3,
2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

Antallet af forskellige permutationer af n elementer er betegnet med P_n og
beregnes med formlen P_n= n!.

Eksempel 8. På hvor mange måder syv bøger
forskellige forfattere kan arrangeres i en række på hylden?Afgørelse:dette problem om nummeret
omarrangering af syv forskellige bøger. Der er P₇= 7!= 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040
måder at arrangere bøger på.

Diskussion. Vi ser,
at antallet af mulige kombinationer kan beregnes efter forskellige regler
(permutationer, kombinationer, placering) og resultatet bliver anderledes,
fordi. princippet om optælling og selve formlerne er forskellige. Ser nøje på
definitioner, kan ses, at resultatet afhænger af flere faktorer
på samme tid.
Først, fra det, fra hvor mange elementer kan vi kombinere dem
sæt (hvor stor er den samlede bestand af elementer).
For det andet, resultatet afhænger af, hvor store er sæt af elementer for os
brug for

Og den sidste, det er vigtigt at vide, er for os
vigtig rækkefølge af varer i et sæt. Lad os forklare den sidste faktor
følgende eksempel

Eksempel 9. På forældremødet
til stede 20 mand. Hvor mange forskellige kompositionsmuligheder er der?
forældreudvalg, hvis det skulle komme ind 5 mand?Afgørelse: I dette eksempel, vi
ikke interesseret i rækkefølgen af ​​navne på udvalgslisten. Hvis som et resultat i hans
kompositionen vil være de samme mennesker, så er betydningen for os den samme
mulighed. Derfor kan vi bruge formlen til at beregne antallet af kombinationer ud fra 20 elementer af 5.
Ting vil være anderledes, hvis hvert komitémedlem oprindeligt er ansvarlig for
bestemt retning af arbejdet. Derefter med den samme lønningsliste
komité, indeni er det muligt 5! permutationsmuligheder, hvilket betyder noget. nummer
forskellige (og sammensætning, og efter ansvarsområde) indstillinger defineret i
i dette tilfælde antallet af placeringer
af 20 elementer af 5.

Selvtestopgaver
1. Hvor mange trecifrede lige tal kan laves ud fra cifre 0, 1, 2, 3, 4, 5,
6, hvis tal kan gentages?
Siden. et lige antal på tredjepladsen kan være 0, 2, 4, 6, dvs.. fire cifre. Ethvert af de syv cifre kan være på andenpladsen. Ethvert af syv cifre undtagen nul kan være i første omgang, dvs.. 6 muligheder. Resultat = 4 * 7 * 6 = 168.
2. Hvor mange femcifrede tal er der, som læser det samme til venstre
højre og højre mod venstre?
Ethvert nummer kan være i første omgang undtagen 0, dvs.. 9 muligheder. Ethvert nummer kan være på andenpladsen, dvs.. 10 muligheder. Ethvert nummer fra, dvs.. 10 muligheder. Det fjerde og femte ciffer er foruddefineret, de matcher det første og det andet, dermed, antallet af sådanne tal er 9 * 10 * 10 = 900.
3. Der er ti emner og fem lektioner om dagen i klassen. På mange måder kan du
lav en tidsplan for en dag?
4. Hvor mange måder du kan vælge 4 delegere til konferencen, hvis i en gruppe
20 mand?

n = C₂₀4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)= 4845.

5. Hvor mange måder kan otte forskellige bogstaver nedbrydes til otte
forskellige konvolutter, hvis der kun lægges et bogstav i hver konvolut?
Du kan lægge i den første konvolut 1 med otte breve, i den anden af ​​de syv tilbageværende, i den tredje af seks osv.. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Tre matematikere og ti økonomer skal bestå af en kommission,
bestående af to matematikere og seks økonomer. Hvor mange måder er det
kan lade sig gøre?

Antal måder at vælge matematik C₃2= 3!/(2!*(3-2))!= 3/2, antal måder at vælge økonom C₁₀6= 10!/(6!*(10-6))!= 7 * 8 * 9 * 10 /(1*2*3*4)= 210. n = C₃2*FRA₁₀6= 3 * 210 = 630.