What is the best lottery

The rule 4. Start on time

PowerBall Lottery Ticket, by the way, worth 2 dollar. To calculate the benefits, which would pay off the purchase of a ticket, you need to multiply the ticket price by 292 201 338.

More about calculations. This is a reference to the first point., where it says, that the benefit of a solution is equal to its value, multiplied by the probability. If we have an event with probability 1 / X and value N, then the benefit will be N / X. We spend 2 dollar and we can count, how much the win would pay off the ticket purchase:

• 2 = N ÷ X.
• N = 2 × X, and X here is just equal 292 201 338, as shown by the calculations from the previous part.

You also need to take into account taxes (discover, what percentage of the declared amount will actually go to the winner, usually it's about 70%). That is, the jackpot must be at least 850 million dollars, and this happens in this lottery. How so, I said at the beginning, that the gain in such a multiplication is always not in favor of the player?

The fact, what if the jackpot has not been drawn, then it goes next time, and that's why money accumulates for a while, and ticket sales continue.

But it is impossible to find out in advance. However, you can start buying tickets, as soon as the size of the jackpot exceeds the mentioned amount. In such a situation, mathematically, the game will be beneficial.

You can still understand, which is more profitable: buy many tickets for one game or buy one ticket for many games? Let's think.

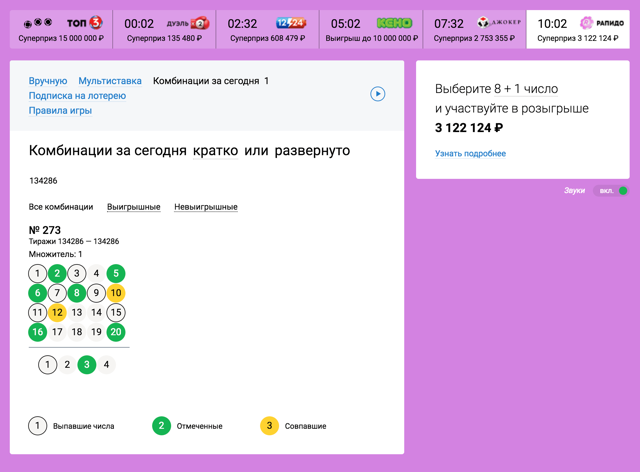
In probability theory there is a concept of unrelated events. It means, that the outcome of one event does not affect the outcome of another. for example, if you roll two dice, then the falling numbers on them are not related: in terms of randomness, one die does not affect the behavior of the other. But if you draw two cards from the deck, then these events are connected, because the first card depends on, what cards will remain in the deck.

A popular misconception about this is called a player error.. It arises from a person's intuitive idea of ​​the connectedness of unrelated events.

Returning to lotteries: different games are unrelated events, because the sequence of balls is re-selected. So the chances of winning any particular lottery do not depend on whether, how many times have you played it before. It is very difficult to accept intuitively., because a person every time, buying a ticket, thinks: “Well, now you're lucky, how long to, I've been playing a lot of time!" But no, probability theory is a heartless thing.

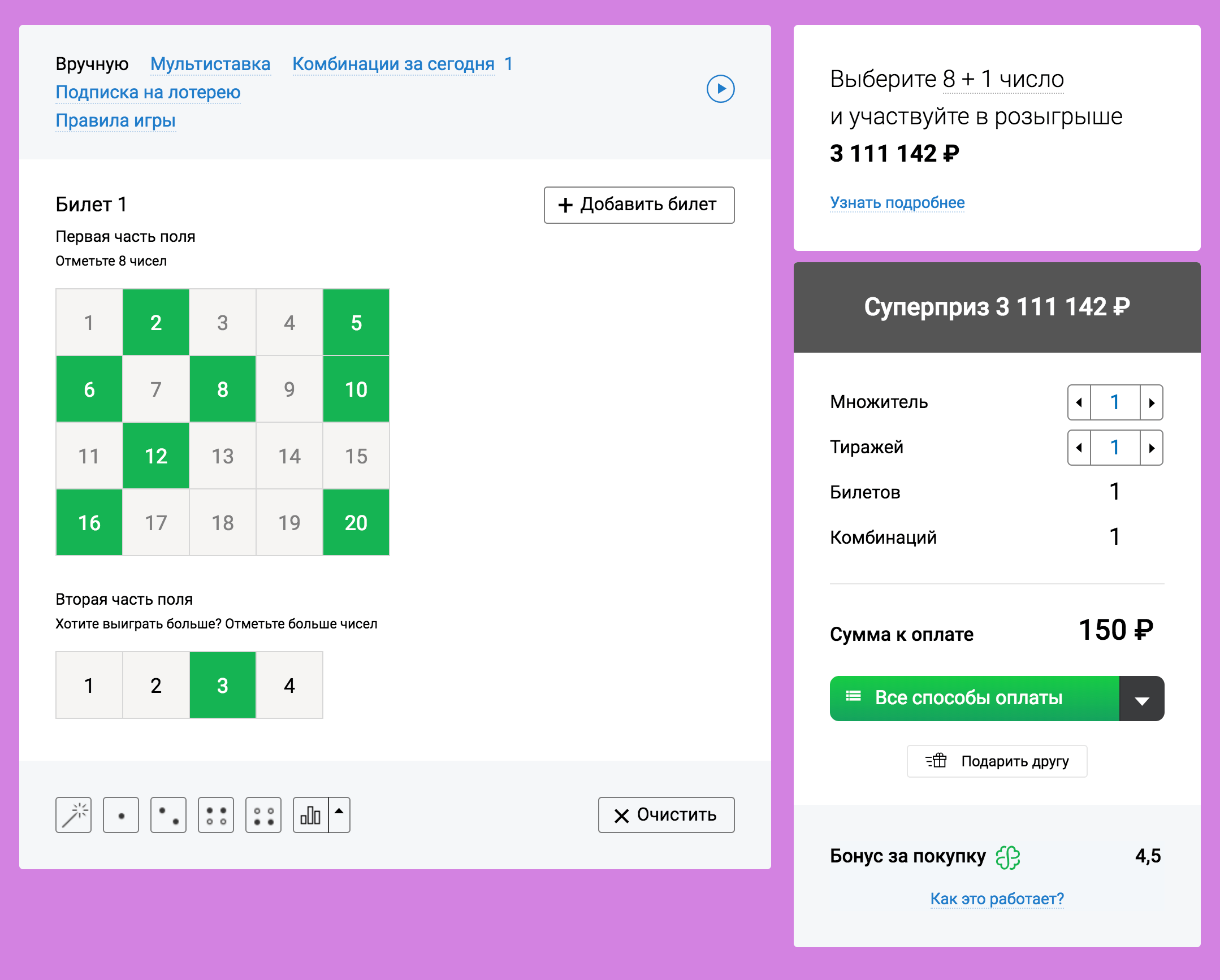
But buying multiple tickets for one game increases your chances proportionally, because tickets inside one game are tied: if one wins, means, other (with another combination) definitely won't win. Purchase 10 tickets increases the chances of 10 time, if all combinations on the tickets are different (in fact, almost always it is). In other words, if you have money for 10 tickets, it's better to buy them for one game, than buy with a ticket to 10 games.

If you just take a ticket from your salary once a month for the sake of, then, likely, the process of playing matters to you. Mathematically, it is more profitable to save this money and buy immediately at the end of the year 12 tickets, although, of course, losing in such a situation will be perceived more devastating.

The rule 1. Assess the risks

It's no secret for a modern enlightened person, that casinos and various gambling establishments calculate all their games as, to always be the winner and make a profit. This is done very simply: the person needs to return the winnings, which correlates with his bet downward compared to his chances of winning.

There are no exceptions, unless someone specifically wants to give you money. Keep this simple rule in mind, to always look at the situation soberly.

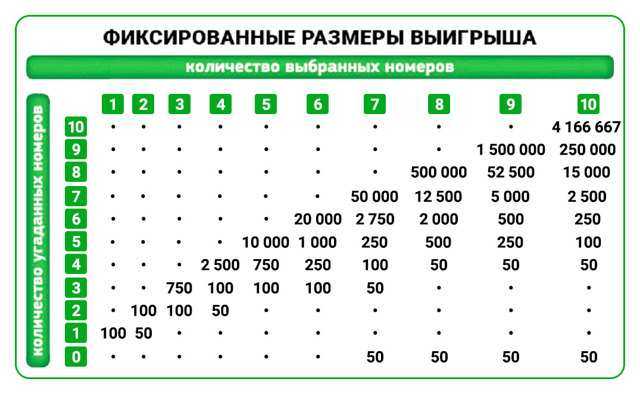
Game theory evaluates any strategy in the same way: the probability of getting a win is multiplied by its size. Roughly speaking, mathematics counts, what is guaranteed to get 1 000 rubles - how to get 2 000 rubles with a 50% chance. This principle gives you the ability to roughly compare different games with each other.. What's better: million dollar with a chance 1/100 000 or 50 dollars with a chance 1/4? It seems intuitive, that the first sentence is more interesting, but the latter is more mathematically advantageous.

If you stay within the framework of math alone, can be calculated: it is impossible to win at the casino, because any chosen strategy leads to, that the product of the probability of winning by the size of the payment for the player is always lower than the bet, which he already did.

And also because, that money is nonlinear for us: formally obtain 1 ruble right now is how to get a million rubles with a chance 1/1 000 000, but in fact, the loss of the ruble will not affect our condition in any way, nothing will change in life, but getting a million is a very serious event.