Cual es la mejor loteria

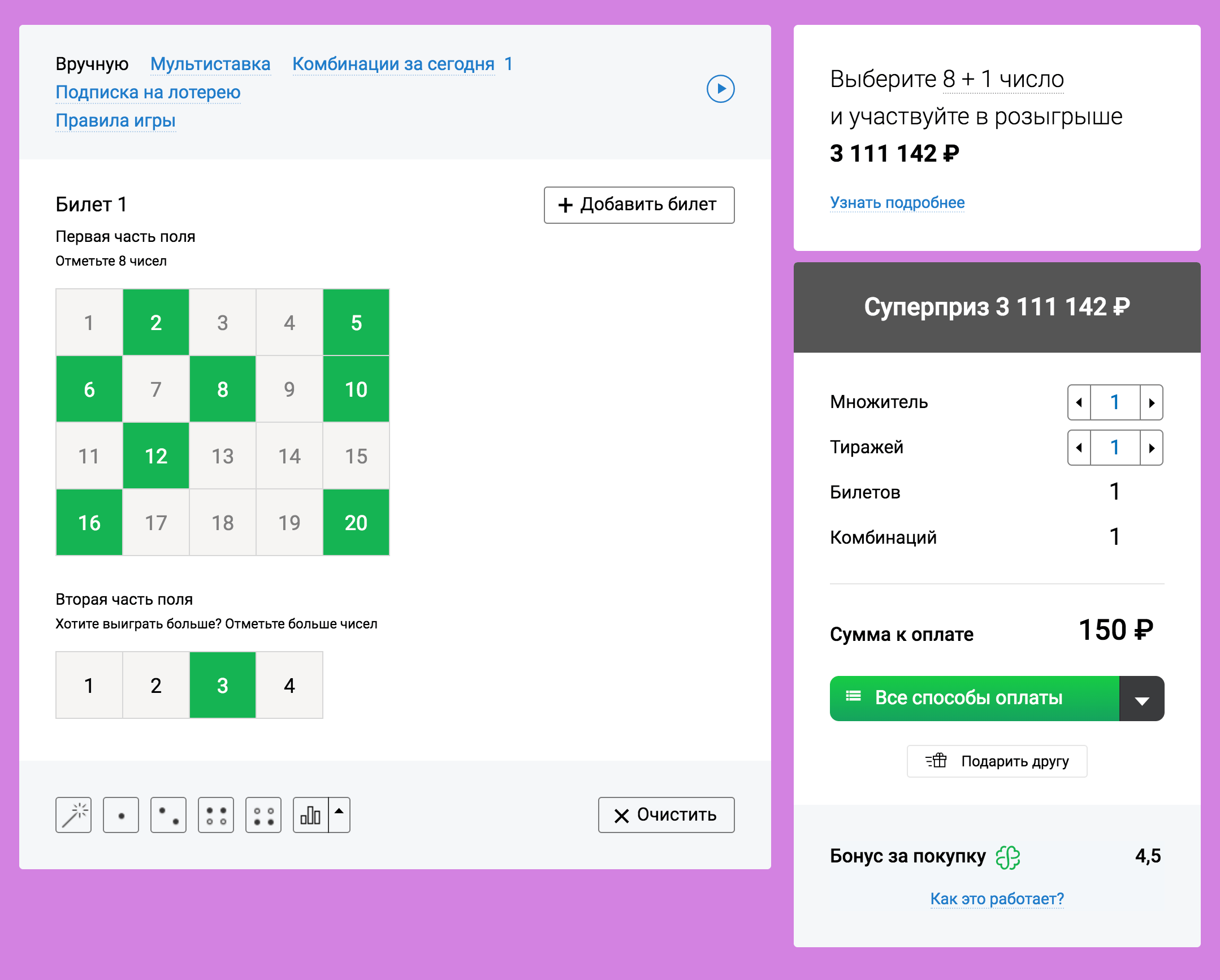
La regla 4. Empiece a tiempo

Billete de lotería PowerBall, por cierto, valor 2 dólar. Para calcular los beneficios, que pagaría la compra de un boleto, нужно умножить цену билета на 292 201 338.

Más sobre cálculos. Esta es una referencia al primer punto., En donde dice, que el beneficio de una solución es igual a su valor, multiplicado por la probabilidad. Si tenemos un evento con probabilidad 1 / X y valor N, entonces el beneficio será N / X. Мы тратим 2 доллара и можем подсчитать, cuánto pagaría la ganancia por la compra del boleto:

• 2 = N ÷ X.
• N = 2 × X, а X тут как раз равен 292 201 338, como se muestra en los cálculos de la parte anterior.

También debes tener en cuenta los impuestos (descubrir, qué porcentaje de la cantidad declarada irá realmente al ganador, normalmente se trata de 70%). То есть джекпот должен составлять как минимум 850 Millón de dólares, y esto pasa en esta lotería. Cómo es eso, Dije al principio, que la ganancia en tal multiplicación no siempre está a favor del jugador?

El hecho, ¿Qué pasa si no se ha sorteado el premio mayor?, luego va la próxima vez, y por eso el dinero se acumula por un tiempo, y la venta de entradas continúa.

Pero es imposible averiguarlo de antemano.. Sin embargo, puedes empezar a comprar entradas., tan pronto como el tamaño del premio mayor exceda la cantidad mencionada. En tal situación, matemáticamente, el juego será beneficioso.

Todavía puedes entender, cual es mas rentable: compre muchos boletos para un juego o compre un boleto para muchos juegos? Pensemos.

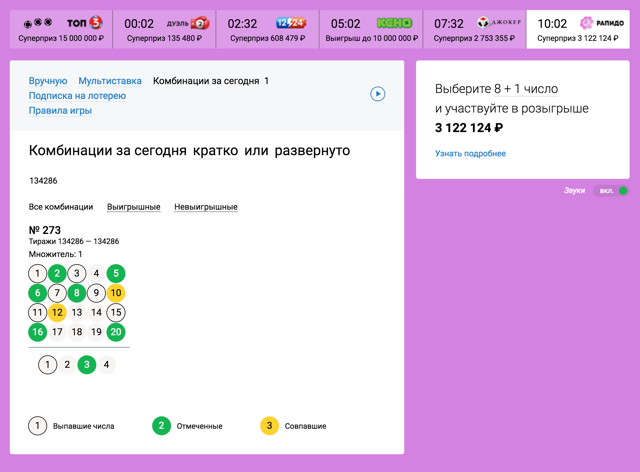
En la teoría de la probabilidad hay un concepto de eventos no relacionados. Significa, que el resultado de un evento no afecta el resultado de otro. por ejemplo, si tiras dos dados, entonces los números que caen en ellos no están relacionados: en términos de aleatoriedad, uno muere no afecta el comportamiento del otro. Pero si sacas dos cartas de la baraja, entonces estos eventos están conectados, porque la primera carta depende de, que cartas quedarán en la baraja.

Un concepto erróneo popular sobre esto se llama error de jugador.. Surge de la idea intuitiva de una persona de la conexión de eventos no relacionados.

Volviendo a las loterías: los diferentes juegos son eventos no relacionados, porque se vuelve a seleccionar la secuencia de bolas. Por tanto, las posibilidades de ganar una lotería en particular no dependen de si, cuantas veces lo has jugado antes. Es muy difícil de aceptar intuitivamente., porque una persona cada vez, comprar un boleto, piensa: "Bueno, ahora tienes suerte, cuanto tiempo, He estado jugando mucho tiempo!" Pero no, la teoría de la probabilidad es una cosa despiadada.

Pero comprar varios boletos para un juego aumenta proporcionalmente tus posibilidades, porque los boletos dentro de un juego están empatados: si uno gana, medio, otro (con otra combinación) definitivamente no ganará. Покупка 10 билетов увеличивает шансы в 10 hora, si todas las combinaciones en los boletos son diferentes (de hecho, casi siempre es). En otras palabras, если у вас есть деньги на 10 Entradas, es mejor comprarlos para un juego, чем покупать по билету на 10 juegos.

Si solo toma un boleto de su salario una vez al mes por el bien de, luego, probable, el proceso de jugar te importa. Математически выгоднее скопить эти деньги и в конце года купить сразу 12 Entradas, a pesar de que, por supuesto, perder en tal situación será percibido como más devastador.

La regla 1. Evaluar los riesgos

No es ningún secreto para una persona iluminada moderna, que los casinos y varios establecimientos de juego calculan todos sus juegos como, ser siempre el ganador y obtener ganancias. Esto se hace de manera muy simple: la persona necesita devolver las ganancias, que se correlaciona con su apuesta negativa en comparación con sus posibilidades de ganar.

No hay excepciones, a menos que alguien específicamente quiera darte dinero. Tenga en cuenta esta sencilla regla, mirar siempre la situación con seriedad.

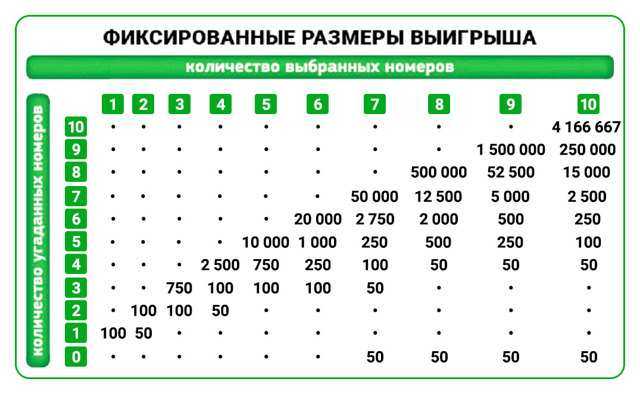
La teoría de juegos evalúa cualquier estrategia de la misma manera: la probabilidad de obtener una victoria se multiplica por su tamaño. Mas o menos, las matemáticas cuentan, что гарантированно получить 1 000 рублей — это как получить 2 000 рублей с 50-процентным шансом. Este principio le brinda la posibilidad de comparar de manera aproximada diferentes juegos entre sí.. Que es mejor: миллион долларов с шансом 1/100 000 o 50 долларов с шансом 1/4? Parece intuitivo, que la primera frase es mas interesante, pero este último es matemáticamente más ventajoso.

Si te quedas solo en el marco de las matemáticas, se puede calcular: es imposible ganar en el casino, porque cualquier estrategia elegida conduce a, que el producto de la probabilidad de ganar por el monto del pago para el jugador es siempre menor que la apuesta, que ya hizo.

Y tambien porque, ese dinero no es lineal para nosotros: формально получить 1 рубль прямо сейчас — это как получить миллион рублей с шансом 1/1 000 000, pero de hecho, la pérdida del rublo no afectará nuestra condición de ninguna manera, nada cambiará en la vida, pero conseguir un millón es un evento muy serio.