Kombinatoriset elementit

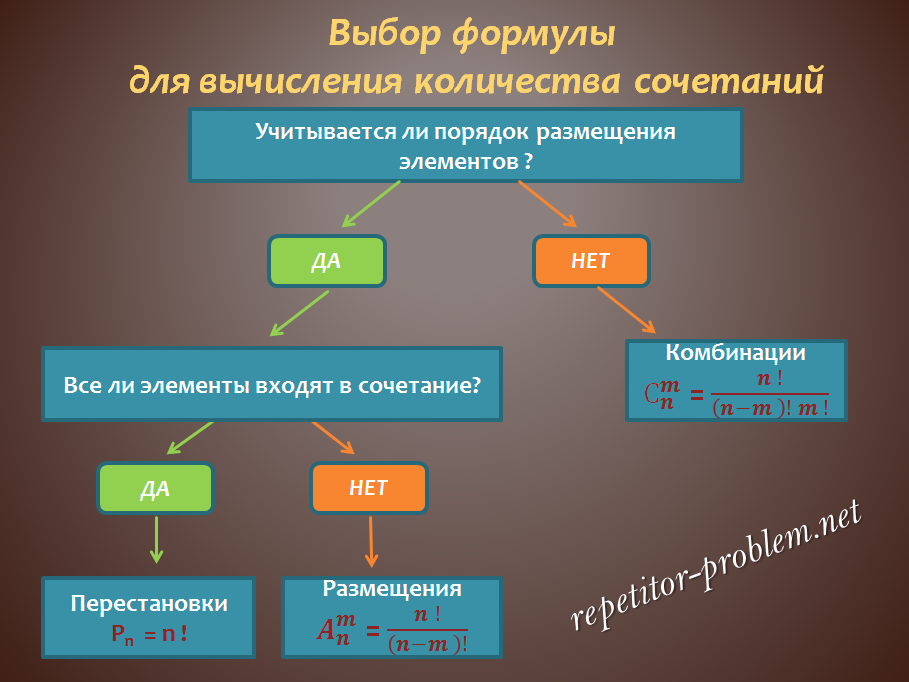
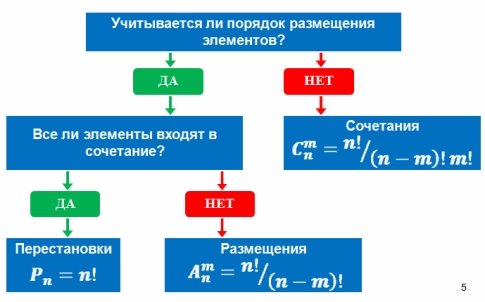
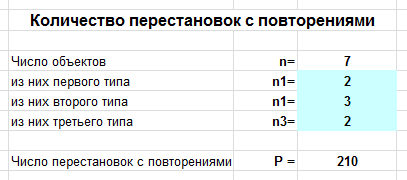
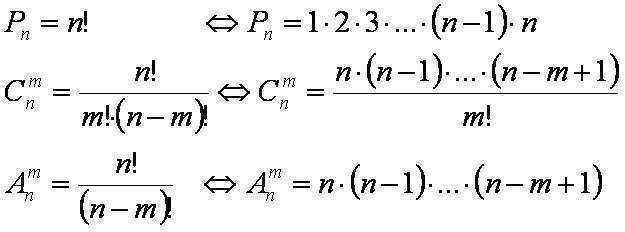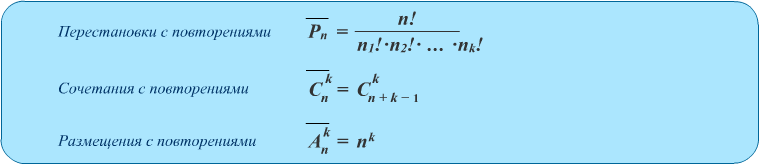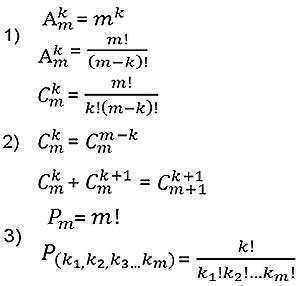Rahan taika numerologiassa

Jokaisella numerolla on oma energiansa ja se vaikuttaa ihmisen elämään tietyllä tavalla.. Rahan numerologia auttaa määrittämään luvun merkityksen, selvitä rahan ja varallisuuden henkilökohtainen koodi. Verotunnus lasketaan syntymäajan mukaan. Sitten sinun täytyy nähdä transkriptio. Sinun on myös tiedettävä, kuinka käyttää varallisuuskoodiasi oikein.

Tärkeintä on laskea rahoituskoodi oikein

sitä paitsi, mikä on varallisuuden määrä, siellä on myös numeroita, ei tuo yltäkylläisyyttä ihmisen elämään. Niitä on vältettävä. Rahoitusvirran houkutteleminen, täytyy tutustua, mitä kukin numero tarkoittaa:

1. Nolla ja yksi. Numerologit uskovat, että nämä numerot ja koodit ovat negatiivisia rahataloudelle, he eivät tuo onnea. Siksi sinun tulisi välttää säästöjä., talletukset määrät, joissa nämä luvut ovat läsnä, koska ne hidastavat kassavirtaa eivätkä tuo vaurautta ja menestystä.
2. Pari. Tämä on onneton hahmo. Hän ei tuo vaurautta ja menestystä. Tämän nimellisarvon seteleitä ei suositella säästöihin, älä kanna niitä lompakossasi.
3. Kolmikko. On taloudellisesti suotuisa, sen avulla henkilö voi voittaa arpajaiset, löytää muita tulolähteitä. Mutta numerologit eivät suosittele varojen keräämistä., jonka summa on 300, 3000, 30000. Tämä luku tarvitsee jatkuvaa liikettä, hän tarvitsee energiaa, ei rauhaa. Parasta on ostaa arpalippu tällaisesta summasta tai sijoittaa se omaan yritykseesi..
4. Henkilökoodissa olevat neljä ovat vakauden symboli, luotettavuus. Ihanteellinen säästöihin, säästöjä, sijoitus on laskujen määrä 400, 4000, 40000. Tällä tavalla, vauraus kasvaa.
5. Viisi on erittäin tärkeä numeerisen varallisuuden koodinumero. Tämän numeron setelit ovat oikean rahan magneetteja.. Ne voidaan lainata, viettää matkaan, kerääntyä, viettää niin, niinkuin haluat.
6. Tällainen rahoituskoodi saattaa aiheuttaa tiettyjä taloudellisia rajoituksia. Tämän kuvan avulla ihmiset oppivat säästämään, hallita menojasi. Määrä 600, 6000 ovat vakauden ja varmuuden symboli. Numerologit eivät suosittele tällaisten summien sijoittamista.
7. Seitsemän on koodi, huono onni, sitä ei voida käyttää varastointiin, investoinnit, säästöjä, lainat ja muut rahoitustapahtumat, jotka liittyvät riskiin.
8. Kahdeksan on vahva varallisuuskoodi numerologiassa, häntä pidetään erittäin onnistuneena. Talletukset määrät 800, 8000, 80000 ovat erittäin onnistuneita, ne houkuttelevat rahaa, kuin magneetti.
9. Yhdeksän on henkisyyden ja sisäisen kehityksen symboli. Rahan keräämistä sen kanssa ei tapahdu, mutta tappiota ei myöskään tule. On suositeltavaa käyttää summat yhdeksän kanssa itseopiskeluun, koulutus

Numeroiden oikea käyttö, tarvitsee tietää, kuinka laskea varallisuuden koodi. Seuraavaksi sinun on selvitettävä säännöt tällaisen yhdistelmän käytöstä.. Saanko rikastua, riippuu paitsi laskennan tuloksena saadusta koodista, mutta myös siitä, kuinka oikein käyttää sitä.

viitetiedot

AsiakirjatRaportitmainitsee Asiakirjapohja SecuritiesVarauksetTalousasiakirjatPäätöslauselmatOtsikko aiheittainRahoitusVenäjän federaation alueiden kaupungit tarkkojen päivämäärien mukaanEhdotTieteellinen terminologia Taloudellinen talousAikaPäivämäärät 2015 2016 Sijoituksen rahoitusalan asiakirjat

Yhdistelmät ilman toistoja

Tehtävä: Löydä kaikki mahdolliset yhdistelmät ilman toistoja monista elementeistä {1,2,3} mennessä 2.
Seuraavia yhdistelmiä on olemassa:1: 1 22: 1 33: 2 3
Mahdollisten yhdistelmien lukumäärä ilman M: n N elementin toistoa voidaan määrittää kaavalla (N ≥M):

että M: ssä! kertaa vähemmän kuin vastaava sijoittelujen määrä ilman toistoja (koska yhdistelmät ilman toistoja eivät riipu elementtien järjestyksestä).
Harkitse ongelmaa saada kaikki yhdistelmät numeroille 1 ... N kirjoittamalla M. Toteutus C ++: ssa

12345678910111213141516171819202122232425262728293031323334353637383940414243

#sisältää <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int k = m; varten (int i = k – 1; i >= 0; –i) jos (a < n – k + i + 1) { ++a; varten (int j = i + 1; j < k; ++j) a = a + 1; return true; } palauta väärä;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; varten (int i = 0; i < n; i++) cout << a << ” “; cout << endl;}int main() { int n, m, *a; cout << “N = “; cin >> n; cout << “M = “; cin >> m; a = new int; varten (int i = 0; i < n; i++) a = i + 1; Print(a, m); jos (n >= m) { sillä aikaa (SeuraavaSet(a, n, m)) Print(a, m); } cin.get(); cin.get(); palata 0;}

Результат выполнения

Englannin numerologia: käsite ja olemus

Vanhin tieto, jotka auttavat selittämään, tulkita sitä, mitä enkelit haluavat kertoa ihmiselle, kutsutaan enkelinumerologiaksi.

Palauttaa mieleen, että numerologia tutkii numeroiden värähtelyjä, numeroa, niiden vaikutus ihmisiin ja elämän prosesseihin. Toinen englantilainen matemaatikko, astrologi John Dee kirjoitti 1500-luvulla teoksen numeroista, jota hän piti universaalisena enkelikielenä ihmisten kanssa kommunikoinnissa.

Enkelinumerologian suhteellisen nuoren opetuksen perustaja on Doreen Verche. Selvänäkijä Amerikasta, psykologi ja filosofi, monien kirjojen kirjoittaja. Hän omisti teoksensa Korkeimmille Olennoille, mukaan lukien jumalat, enkelit, pyhät. Monien vuosien ajan hän on tutkinut selittämättömiä ilmiöitä.. Mutta se oli sen arvoista. Hän loi instrumentin, kuka voi auttaa sinua tulkitsemaan taivaasta avustajien viestit. Doreen Vercen mukaan, saamme säännöllisesti merkkejä enkeleiltä, jotka varoittavat vaaroista, ehdottaa ratkaisuja ihmisen elämän ongelmiin.

Enkelit puhuvat ihmiselle numeroilla, kirjaimet, merkkejä. Doreen Vercen teokset puhuvat näkymättömien pitäjien vihjeistä, jotka on koodattu toistuvina numeroina tai niiden yhdistelminä. Nimittäin:

• auton rekisterikilvissä;
• kellossa;
• brownie, huoneisto, toimiston numerointi;
• syntymäpäivinä;
• lippulomakkeissa, kuin liikenteessä, ja julkiset tilat jne..

Kaikissa tällaisissa yhdistelmissä, luvut piilottavat tietoja, kuka voi tehdä muutoksia ihmisten tulevaisuuteen. Doreen Verce on tehnyt paljon tutkimusta aiheesta, omistettu numerologisille laskelmille syntymäpäivän mukaan. Tällaiset laskelmat auttavat tunnistamaan lapset., joilla on ainutlaatuiset kyvyt syntymästä asti, eikä vain.

Numerovastaavuudet, yhdistelmiä, joita emme usein huomaa

Mutta se on syytä kiinnittää huomiota, koska tällainen ilmiö voi olla tärkeä varoitus. Loppujen lopuksi enkelit eivät lähetä meille tällaista merkkiä turhaan

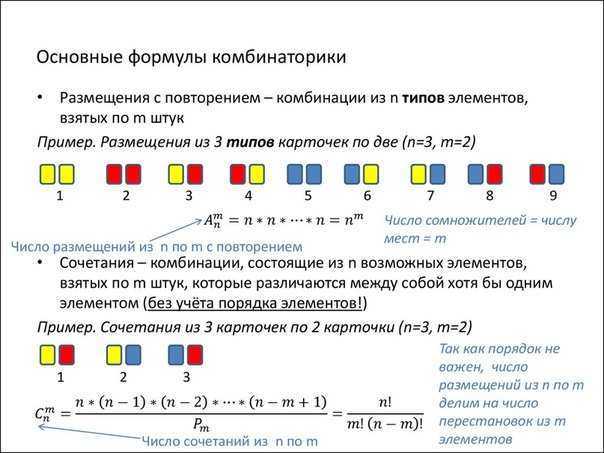
Yhdistelmät toistojen kanssa

Yhdistelmät toistojen kanssa ovat M-elementtien sarjoja, jossa joukko N: n kukin elementti voi osallistua useita kertoja. Tässä tapauksessa ei aseteta rajoituksia M: n ja N: n arvojen suhteelle, ja toistojen yhdistelmien kokonaismäärä on

Esimerkki tällaisesta ongelmasta on M-postikorttien valinta N: ltä kaikilla mahdollisilla tavoilla.

Jos haluat luoda yhdistelmiä toistojen kanssa, käytämme ratkaisua sijoittelujen luomiseen toistoilla., C ++ -toteutus

1234567891011121314151617181920212223242526272829303132333435363738394041

#sisältää <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int j = m – 1; sillä aikaa (a == n && j >= 0) j–; jos (j < 0) palauta väärä; jos (a >= n) j–; a++; jos (j == m – 1) return true; varten (int k = j + 1; k < m; k++) a = a; return true;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; varten (int i = 0; i < n; i++) cout << a << ” “; cout << endl;}int main() { int n, m, *a; cout << “N = “; cin >> n; cout << “M = “; cin >> m; int h = n > m ? n : m; // размер массива а выбирается как max(n,m) a = new int; varten (int i = 0; i < h; i++) a = 1; Print(a, m); sillä aikaa (SeuraavaSet(a, n, m)) Print(a, m); cin.get(); cin.get(); palata 0;}

Edellä olevan algoritmin tulos:

Algoritmointi

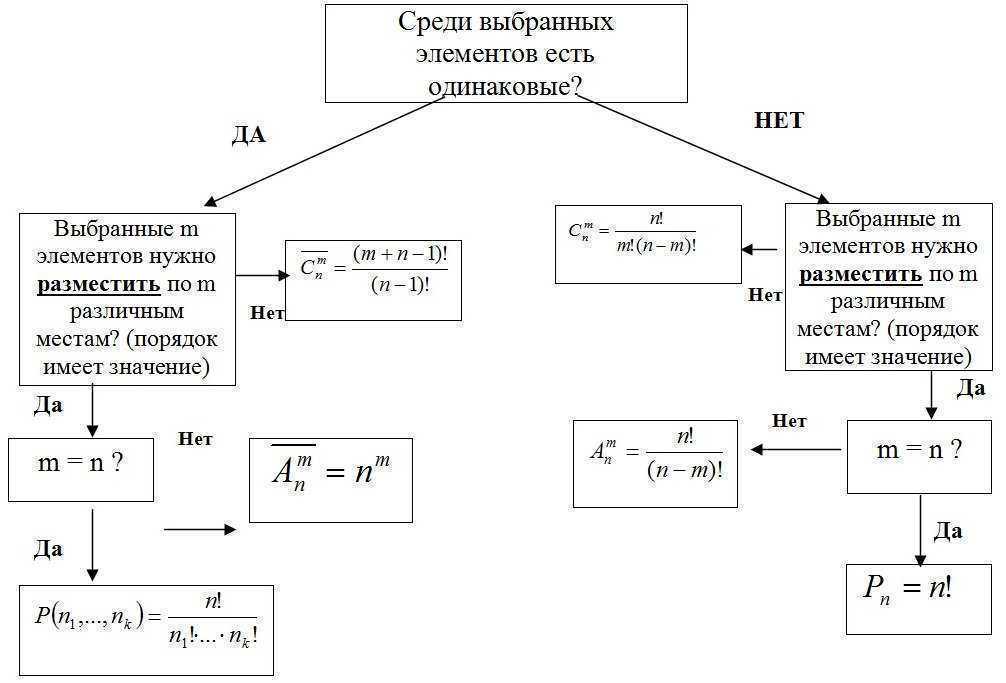
Kombinatorian peruskaava

Olkoon k elementtiryhmiä, ja i: s ryhmä koostuu n: stä_i elementtejä.
Valitse yksi elementti kustakin ryhmästä. Sitten tapausten kokonaismäärä N,
jolla tällainen valinta voidaan tehdä, määritetään suhteella N = n₁*n₂*n₃*…*n_k.

Esimerkki 1. Selitetään tämä sääntö yksinkertaisella tavalla
esimerkki. Olkoon kaksi ryhmää elementtejä, ja ensimmäinen ryhmä koostuu
n₁ elementtejä, ja toinen – n: stä₂ elementtejä. kuinka monta
näistä kahdesta ryhmästä voidaan muodostaa eri elementtiparit, tällä tavalla,
niin että kummassakin ryhmässä on yksi elementti parissa? Tunnustetaan, Otimme
ensimmäisen ryhmän ensimmäinen elementti ja, muuttamatta sitä, kävi läpi kaikki mahdolliset
parit, vain toisen ryhmän elementtien muuttaminen. Tällaiset parit tälle elementille
voi olla n₂. Sitten otamme toisen kohteen ensimmäisestä ryhmästä
ja säveltää myös kaikki mahdolliset parit. Tällaisia ​​pareja on myös n₂.
Koska ensimmäinen ryhmä sisältää vain n₁ elementti, kaikki mahdolliset
vaihtoehtoja on n₁*n₂.Esimerkki 2. kuinka monta
kolminumeroiset parilliset numerot voivat koostua numeroista 0, 1, 2, 3, 4, 5, 6, jos
numerot voidaan toistaa?Päätös: n₁= 6
(koska. ensimmäisenä numerona voit ottaa minkä tahansa numeron 1, 2, 3, 4, 5, 6), n₂= 7
(koska. toisena numerona voit ottaa minkä tahansa numeron 0, 1, 2, 3, 4, 5,
6), n₃= 4 (koska. kolmanneksi numeroksi voit ottaa minkä tahansa numeron 0, 2, 4,
6).

niin, N = n₁*n₂*n₃= 6 * 7 * 4 = 168.

Siinä tapauksessa, kun kaikilla ryhmillä on sama määrä elementtejä, eli. n₁= n₂=…n_k= n
sitä voitaisiin harkita, että jokainen valinta tehdään samasta ryhmästä, lisäksi
elementti valinnan jälkeen palaa taas ryhmään. Sitten kaikkien tapojen määrä
valinta on nk. Tämäntyyppistä valintaa kombinaattorissa kutsutaan valinnaksi paluu.

Esimerkki 3. Kuinka monta on kaikki nelinumeroisia lukuja
voi koostua numeroista 1, 5, 6, 7, 8?Päätös. Jokaiselle listalle
nelinumeroinen luku on viisi mahdollisuutta, tarkoittaa N = 5 * 5 * 5 * 5 = 54 = 625.

Harkitse sarjaa, koostuu n elementistä. se
Kombinatorian joukkoa kutsutaan yleiseksi
aggregaatti.

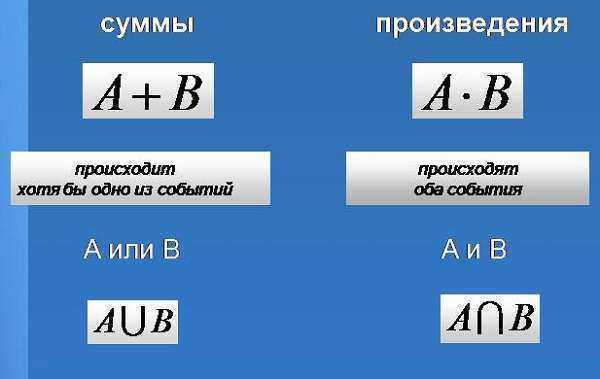
Liiketoiminta ja rahoitus

PankitRikkaus ja hyvinvointiKorruptio(Rikos)MarkkinointiHallintoSijoituksetTakauksetHallintoJulkiset osakeyhtiötProjektitDokumentitVakuudet – valvoa arvopapereita – Arvostusjoukkovelkakirjat Valuutta Kiinteistöt(Vuokrata)AmmatitTyötTradingServicesRahoitusVakuutusBudjettiRahoituspalvelut

Mitä tehdä mantrikoodilla rituaalin suorittamisen jälkeen

Jälkeen, kuinka lukuarvot luettiin aikana 77 päivää, heitä pitäisi syyttää 4 elementtejä jatkotyötä varten.

Tätä varten sinun on suoritettava yksinkertaisia ​​manipulaatioita.:

1. Aktivoi koodi maapallon energialla. Pieni maaperä sopii rituaaliin.. Tarvitset myös kukan siemeniä. Näiden pitäisi olla täsmälleen siemenet., ei kasvien versoja ja mukuloita. Valmisteltuasi tarvittavat määritteet, mantra olisi kirjoitettava tyhjälle paperille ja haudattava maahan, sanomalla sanat kolme kertaa - ”Maa on täynnä rikkauksia, olet nyt unelmani ”. Seuraavaksi ruukkuun asetetaan kukka siemen.
2. Maan alkuaineen jälkeen mantra ladataan veden energialla. Tämä rituaali koostuu siemenen kastelusta, jonka mukana on sanat “vesi ja maa, elvyttää siemenet ”. Kuten edellisessä tapauksessa, antaa lausunto 3 ajat.
3. Seuraavaksi tulee Air-elementtien vuoro. Potti tulevan kasvin kanssa tulisi viedä avoimeen ikkunaan ja sanoa: "Sinä, Ilmaa, tarvitsen, kuin valo, ja anna unelmani Dawn ". Se on toistettava sisällä 3 päivää.
4. Kun siemen itää ilmestyy, on tulipalojen aika. Mantran herättämiseksi tarvitaan uusi sytytetty kynttilä. Se on sijoitettava laitoksen viereen ja, keskittyminen, sanoa kolme kertaa: "Se palaa, Antaa potkut, kynttilä - palaa, ja tuhoaa köyhyyden. Anna verson kasvaa, mitä rahat piiloutuvat. Ja minä kukoistan hänen kanssaan, houkutella varallisuutta rahaan ".

Näiden vaiheiden jälkeen valuuttakoodi alkaa toimia. On suositeltavaa olla heittämättä potti itää ja mantraa, jatkamalla laitoksen tavanomaista hoitoa.

sitä paitsi, parantaa mantrikoodin vaikutusta, voit käyttää numeroiden kuvaa pahviarkilla vihreällä ja punaisella musteella. Tällainen rahatalisman on oltava jatkuvasti mukanasi..

Tunnettujen asioiden taika

Satunnaislukugeneraattorimme verkossa.

Satunnaistingeneraattorimme ei vaadi sen lataamista henkilökohtaiselle tietokoneellesi. Kaikki tapahtuu online-numerogeneraattoritilassa. Määritä vain nämä parametrit, kuten: valikoima numeroita verkossa, missä luvut valitaan satunnaisesti. Ilmoita myös numeroiden määrä, joka valitaan.
Esimerkiksi, у Вас есть группа Вконтакте. В группе вы разыгрываете 5 palkinnot, osallistujien keskuudessa, kuka julkaisee levyn uudelleen. Erillisen sovelluksen käyttäminen, saimme luettelon osallistujista. Jokaiselle on annettu järjestysnumero online-numeroille.

Mene nyt online-generaattoriin ja määritä numeroalue (osallistujien määrä). esimerkiksi, kysyä, mitä numeroita verkossa tarvitaan 5, koska meillä on 5 palkinnot. Теперь жмем кнопку генерации. Sitten saamme 5 satunnaislukuja verkossa, vaihtelevat 1 että 112 mukaan lukien. Luotu 5 verkossa olevat numerot vastaavat viiden osanottajan sarjanumeroa, joista tuli piirustuksen voittajia. Kaikki on yksinkertaista ja kätevää.

Toinen satunnaislukugeneraattorin plus on, että kaikki online-numerot annetaan satunnaisesti. Eli vaikuttaa häneen, tai laskea, mikä numero tulee seuraavaksi, ei vaikuta mahdolliselta. Voidaan sanoa, mitä generaattori tekee, rehellinen ja luotettava, ja hallinto, joka jakaa palkintoja ilmaisella generaattorillamme, rehellinen ja kunnollinen kilpailun osallistujien edessä. Ja jos olet epävarma ratkaisusta, sitten voit käyttää kyllä ​​tai ei vastausvälineitä.

Kuinka laskea varallisuuden koodi

On olemassa hyviä ja huonoja yhdistelmiä

Numerologia ja raha liittyvät läheisesti toisiinsa. On numeroyhdistelmiä, vaurautta tuottava, mutta on epäonnistuneita yhdistelmiä. Jos käytät niitä oikein, menestys ja onni ovat teidän puolellanne. Koodin laskeminen on helppoa. Tätä varten sinun on suoritettava seuraavat laskelmat:

• kirjoita numero tyhjälle paperille, syntymäkuukausi ja -vuosi (esim, 31.10.1987);
• onnistumisarvon laskemiseksi, kaksi ensimmäistä numeroa tulisi lisätä, ts, tietty syntymäaika (esim, 31 - 3 + 1 = 4). Tämä numero on ensimmäinen yhdistelmässä;
• laskea yhdistelmän toinen merkki, on tarpeen laskea kuukauden arvo (esim, lokakuu, 10 kuukausi - 1 + 0 = 1);
• nyt sinun on laskettava syntymävuoden määrä (esim, 1987 - 1 + 9 + 8 + 7 = 25, 2+5= 7);
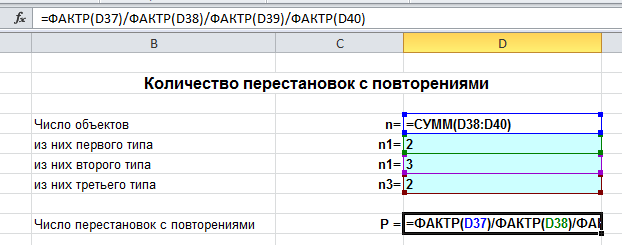
• lopussa sinun on laskettava henkilökohtaisesti yhdistelmän viimeinen merkki, tätä varten kaikki kolme aikaisemmin vastaanotettua numeroa lasketaan yhteen (esim, 4+1+7= 12, 1+2= 3, tässä tapauksessa rahayhdistelmä on 4173). Tuloksena oleva yhdistelmä on henkilön henkilökohtainen koodi..

Henkilökoodin lisäksi, on universaaleja arvoja, jota kaikki voivat hakea, kuin miljonääri, ja keskitulolla. Tämä on digitaalinen maskotti, joka on kuvattu neljän samankokoisen kahdeksan muodossa. Tämä yhdistelmä on erittäin vahva, tarkoittaa rahallista menestystä ja vakautta.

Voit myös laskea sitten, olenko rikas, nimeltä. Tätä varten otetaan taulukko kirjainten ja numeroiden välillä. Esimerkiksi, Marina, joka syntyi 5 numerot. Tässä tapauksessa vain syntymäpäivä pidetään:

M-5, A-1, R-9, I-1, N-6, A-1. 5+1+9+1+6+1= 23, 2+3= 5. Lisää seuraavaksi syntymäaika - 5 + 5 = 10, 1+0= 1 - yksi ja on tietyn henkilön onnen ja rahan koodi. Mutta voiko hän menestyä, riippuu, kuinka hyvin sitä käytetään.

N elementin permutaatiot

Määritelmä 3. Permutaatio
n elementistä
mitä tahansa tilattua sarjaa kutsutaan
nämä elementit.

Esimerkki 7a. Kaikenlaisia ​​permutaatioita
monien joukossa, koostuu kolmesta elementistä {1, 2, 3} ovat: (1, 2, 3), (1, 3,
2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

N elementin erillisten permutaatioiden lukumäärä on merkitty P: llä_n ja
lasketaan kaavalla P_n= n!.

Esimerkki 8. Kirjassa Kuinka monella tapaa seitsemän kirjaa
eri tekijät voidaan järjestää yhdelle riville hyllylle?Päätös:tämä ongelma numerosta
järjestämällä uudelleen seitsemän erilaista kirjaa. On P₇= 7!= 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040
tapoja järjestää kirjoja.

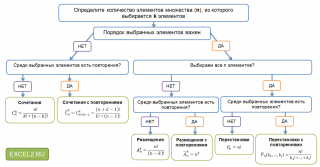
Keskustelu. Me näemme,
että mahdollisten yhdistelmien määrä voidaan laskea eri sääntöjen mukaisesti
(permutaatiot, yhdistelmiä, sijoittelu) ja tulos on erilainen,
koska. laskentaperiaate ja itse kaavat ovat erilaiset. Tarkastellaan tarkasti
määritelmät, voidaan nähdä, että tulos riippuu useista tekijöistä
samaan aikaan.
Ensiksi, siitä, kuinka monesta elementistä voimme yhdistää ne
sarjat (kuinka suuri on alkuaineiden kokonaispopulaatio).
toiseksi, tulos riippuu, kuinka suuria elementtijoukot ovat meille
tarve

Ja viimeinen, on tärkeää tietää, on meille
olennainen tuotteiden järjestys sarjassa. Selitetäänpä viimeinen tekijä
seuraava esimerkki

Esimerkki 9. Vanhempien kokouksessa
esittää 20 mies. Kuinka monta eri sävellysvaihtoehtoa on olemassa
vanhempien komitea, jos sen pitäisi tulla 5 mies?Päätös: Tässä esimerkissä me
ei kiinnosta nimien järjestystä valiokunnan luettelossa. Jos seurauksena hänen
sävellys on samat ihmiset, silloin merkitys meille on sama
vaihtoehto. Siksi voimme käyttää kaavaa laskeaksesi yhdistelmien lukumäärän 20 elementit 5.
Asiat ovat erilaisia, jos jokainen valiokunnan jäsen on alun perin vastuussa
selvä työn suunta. Sitten samalla palkkasummalla
komitea, sen sisällä on mahdollista 5! permutaatiovaihtoehdot, mikä asia. määrä
eri (ja koostumus, ja vastuualueen mukaan) kohdassa määriteltyjä vaihtoehtoja
tässä tapauksessa sijoittelujen määrä
/ 20 elementit 5.

Itsetestaustehtävät
1. Kuinka monta kolminumeroista parillista numeroa voidaan tehdä 0, 1, 2, 3, 4, 5,
6, jos numerot voidaan toistaa?
Siitä asti kun. parillinen luku kolmannella sijalla voi olla 0, 2, 4, 6, eli. neljä numeroa. Mikä tahansa seitsemästä numerosta voi olla toisella sijalla. Mikä tahansa seitsemästä muusta numerosta kuin nolla voi olla ensinnäkin, eli. 6 mahdollisuudet. Tulos = 4 * 7 * 6 = 168.
2. Kuinka monta viisinumeroista numeroa siellä on, jotka lukevat saman vasemmalla
oikealta ja oikealta vasemmalle?
Mikä tahansa numero voi olla ensinnäkin paitsi 0, eli. 9 mahdollisuudet. Mikä tahansa numero voi olla toisella sijalla, eli. 10 mahdollisuudet. Mikä tahansa numero, eli. 10 mahdollisuudet. Neljäs ja viides numero on ennalta määritelty, ne vastaavat ensimmäistä ja toista, siten, tällaisten numeroiden lukumäärä on 9 * 10 * 10 = 900.
3. Luokassa on kymmenen ainetta ja viisi oppituntia päivässä. Voit monin tavoin
tee aikataulu yhdelle päivälle?
4. Kuinka monta tapaa voit valita 4 edustaja konferenssiin, jos ryhmässä
20 mies?

n = C₂₀4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)= 4845.

5. Kuinka monella tavalla kahdeksan erilaista kirjainta voidaan hajottaa kahdeksaksi
erilaisia ​​kirjekuoria, jos kuhunkin kirjekuoreen laitetaan vain yksi kirjain?
Voit laittaa ensimmäisen kirjekuoren 1 kahdeksasta kirjaimesta, toisessa jäljellä olevasta seitsemästä, kolmannessa yksi kuudesta jne.. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Kolmen matemaatikon ja kymmenen taloustieteilijän on oltava palkkiota,
koostuu kahdesta matemaatikosta ja kuudesta ekonomistista. Kuinka monella tapaa se on
voidaan tehdä?

Matematiikan valintatapojen määrä C₃2= 3!/(2!*(3-2))!= 3/2, useita tapoja valita ekonomisti C₁₀6= 10!/(6!*(10-6))!= 7 * 8 * 9 * 10 /(1*2*3*4)= 210. n = C₃2*Alkaen₁₀6= 3 * 210 = 630.