Mikä on paras arpajaiset

Sääntö 4. Aloita ajoissa

PowerBall-arpajaislippu, muuten, arvoinen 2 dollari. Etujen laskemiseksi, mikä maksaisi lipun ostamisen, нужно умножить цену билета на 292 201 338.

Lisätietoja laskelmista. Tämä on viittaus ensimmäiseen kohtaan., missä se sanoo, että ratkaisun hyöty on yhtä suuri kuin sen arvo, kerrottuna todennäköisyydellä. Jos meillä on tapahtuma, jonka todennäköisyys on 1 / X ja arvo N, silloin hyöty on N / X. Мы тратим 2 доллара и можем подсчитать, kuinka paljon voitto maksaisi lipun oston:

• 2 = N ÷ X.
• N = 2 × X, а X тут как раз равен 292 201 338, kuten edellisen osan laskelmat osoittavat.

Sinun on myös otettava huomioon verot (löytää, kuinka suuri prosenttiosuus ilmoitetusta summasta menee voittajalle, yleensä siitä on kyse 70%). То есть джекпот должен составлять как минимум 850 miljoona dollaria, ja tämä tapahtuu tässä arpajaisessa. Kuinka niin, Sanoin alussa, että tällaisen kertolaskun voitto ei aina ole pelaajan eduksi?

Tosiasia, mitä jos jättipottia ei ole nostettu, sitten se menee seuraavalla kerralla, ja siksi rahaa kertyy hetkeksi, ja lippujen myynti jatkuu.

Mutta on mahdotonta selvittää etukäteen. Voit kuitenkin alkaa ostaa lippuja, heti kun jättipotin koko ylittää mainitun määrän. Tällaisessa tilanteessa peli on matemaattisesti hyödyllinen.

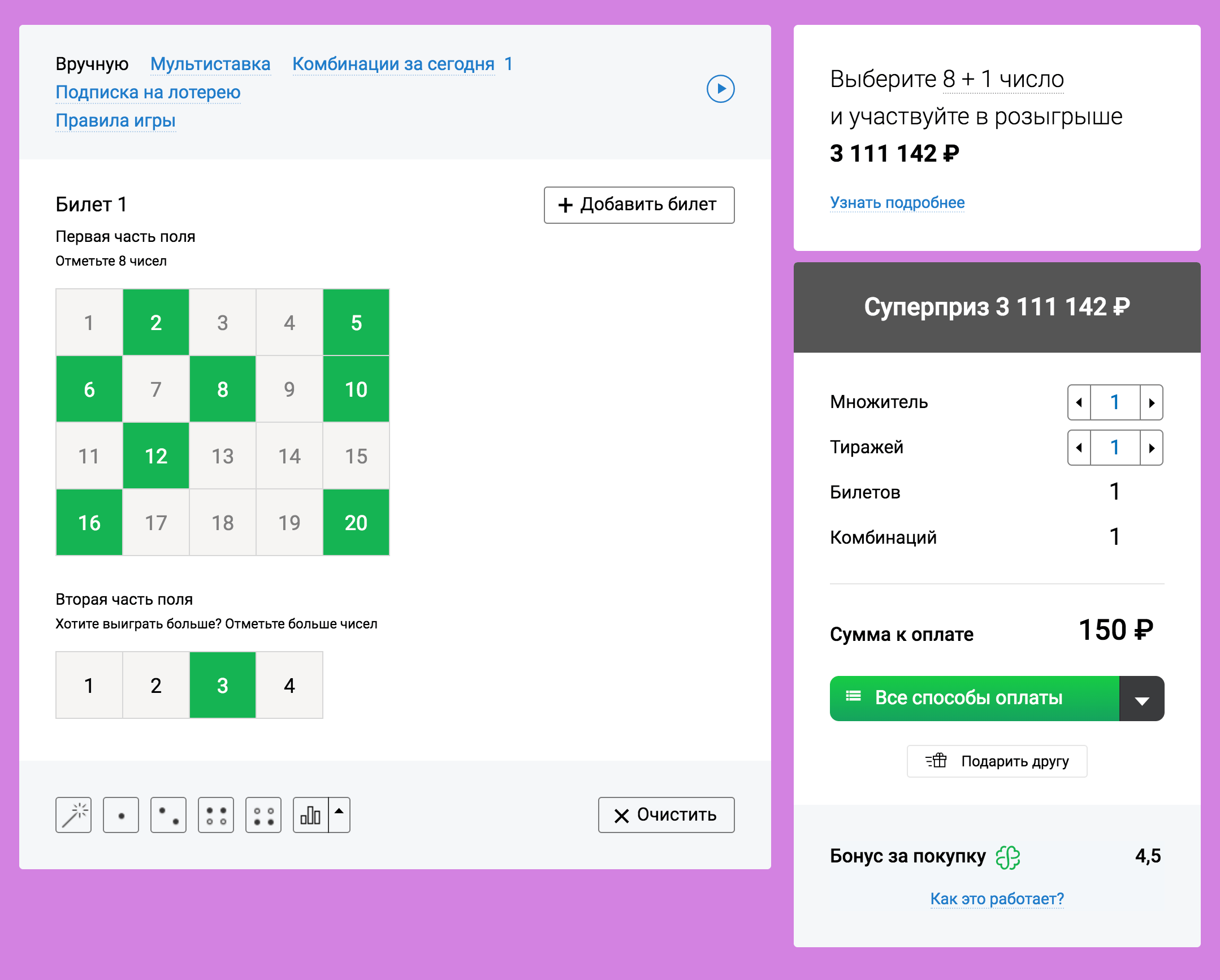
Voit silti ymmärtää, mikä on kannattavampaa: osta useita lippuja yhteen peliin tai osta yksi lippu moniin peleihin? Mietitään.

Todennäköisyysteoriassa on käsite riippumattomista tapahtumista. Se tarkoittaa, että yhden tapahtuman tulos ei vaikuta toisen tulokseen. esimerkiksi, jos heität kaksi noppaa, silloin niiden laskevat numerot eivät ole yhteydessä toisiinsa: satunnaisuuden suhteen, yksi kuolema ei vaikuta toisen käyttäytymiseen. Mutta jos vedät kaksi korttia kannelta, sitten nämä tapahtumat ovat yhteydessä toisiinsa, koska ensimmäinen kortti riippuu, mitkä kortit jäävät kannelle.

Suosittua väärinkäsitystä tästä kutsutaan pelaajan virheeksi.. Se syntyy ihmisen intuitiivisesta käsityksestä toisiinsa liittymättömien tapahtumien kytkeytymisestä.

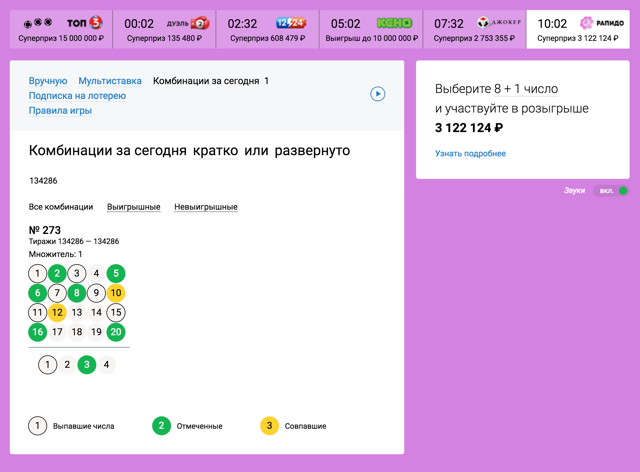
Palataan arpajaisiin: eri pelit eivät liity toisiinsa, koska pallojen järjestys valitaan uudelleen. Joten mahdollisuudet voittaa tietty arpajaiset eivät riipu siitä, kuinka monta kertaa olet pelannut sitä aiemmin. On hyvin vaikeaa hyväksyä intuitiivisesti., koska henkilö joka kerta, osta lippu, ajattelee: ”No, nyt olet onnekas, kuinka kauan, Olen pelannut paljon aikaa!" Mutta ei, todennäköisyysteoria on sydämetön asia.

Useiden lippujen ostaminen yhteen peliin lisää kuitenkin mahdollisuuksiasi suhteellisesti, koska yhden pelin liput ovat sidottuja: jos joku voittaa, tarkoittaa, muut (toisen yhdistelmän kanssa) ei varmasti voita. Покупка 10 билетов увеличивает шансы в 10 aika, jos kaikki lippujen yhdistelmät ovat erilaiset (itse asiassa melkein aina on). Toisin sanoen, если у вас есть деньги на 10 lippuja, on parempi ostaa ne yhdelle pelille, чем покупать по билету на 10 pelejä.

Jos otat vain lipun palkastasi kerran kuukaudessa, sitten, todennäköisesti, soittoprosessi on sinulle tärkeä. Математически выгоднее скопить эти деньги и в конце года купить сразу 12 lippuja, siitä huolimatta, tietysti, häviäminen tällaisessa tilanteessa koetaan tuhoisammaksi.

Sääntö 1. Arvioi riskit

Se ei ole mikään salaisuus nykyajan valaistuneelle henkilölle, että kasinot ja erilaiset rahapelilaitokset laskevat kaikki pelinsä, olla aina voittaja ja ansaita voittoa. Tämä tehdään hyvin yksinkertaisesti: henkilön on palautettava voitot, mikä korreloi hänen panoksensa alaspäin verrattuna hänen voittomahdollisuuksiin.

Ei ole poikkeuksia, ellei joku nimenomaan halua antaa sinulle rahaa. Pidä tämä yksinkertainen sääntö mielessä, tarkastella tilannetta aina järkevästi.

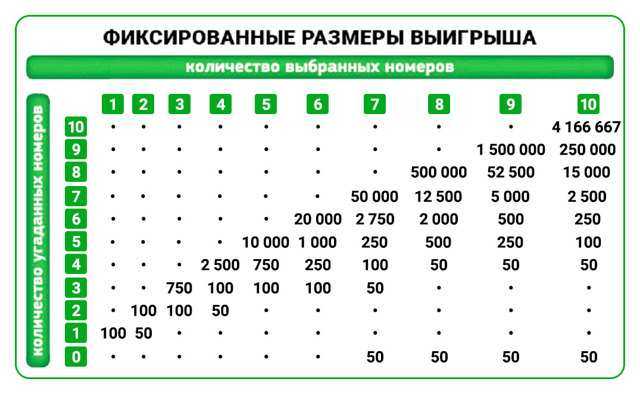
Peliteoria arvioi kaikki strategiat samalla tavalla: todennäköisyys voittaa kerrotaan sen koolla. Karkeasti ottaen, matematiikka laskee, что гарантированно получить 1 000 рублей — это как получить 2 000 рублей с 50-процентным шансом. Tämä periaate antaa sinulle mahdollisuuden verrata karkeasti eri pelejä keskenään.. Mikä on parempi: миллион долларов с шансом 1/100 000 tai 50 долларов с шансом 1/4? Se näyttää intuitiiviselta, että ensimmäinen lause on mielenkiintoisempi, mutta jälkimmäinen on matemaattisesti edullisempi.

Jos pysyt matematiikan puitteissa yksin, voidaan laskea: kasinossa on mahdotonta voittaa, koska mikä tahansa valittu strategia johtaa, että voittotodennäköisyyden tulo pelaajan maksun suuruuden mukaan on aina pienempi kuin veto, jonka hän jo teki.

Ja myös siksi, että raha on epälineaarinen meille: формально получить 1 рубль прямо сейчас — это как получить миллион рублей с шансом 1/1 000 000, mutta itse asiassa ruplan menetys ei vaikuta millään tavalla tilaan, mikään ei muutu elämässä, mutta miljoonan saaminen on erittäin vakava tapahtuma.