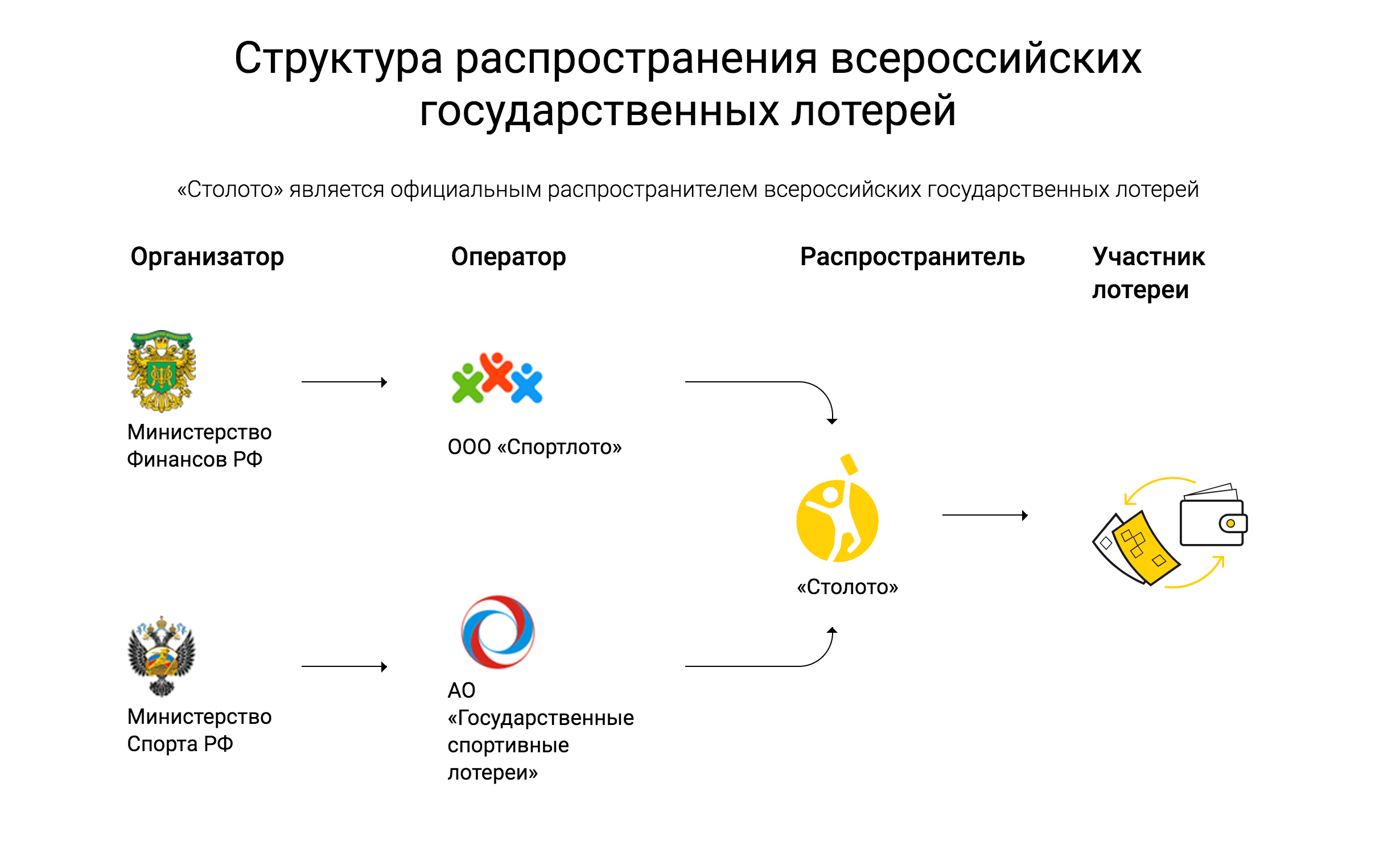
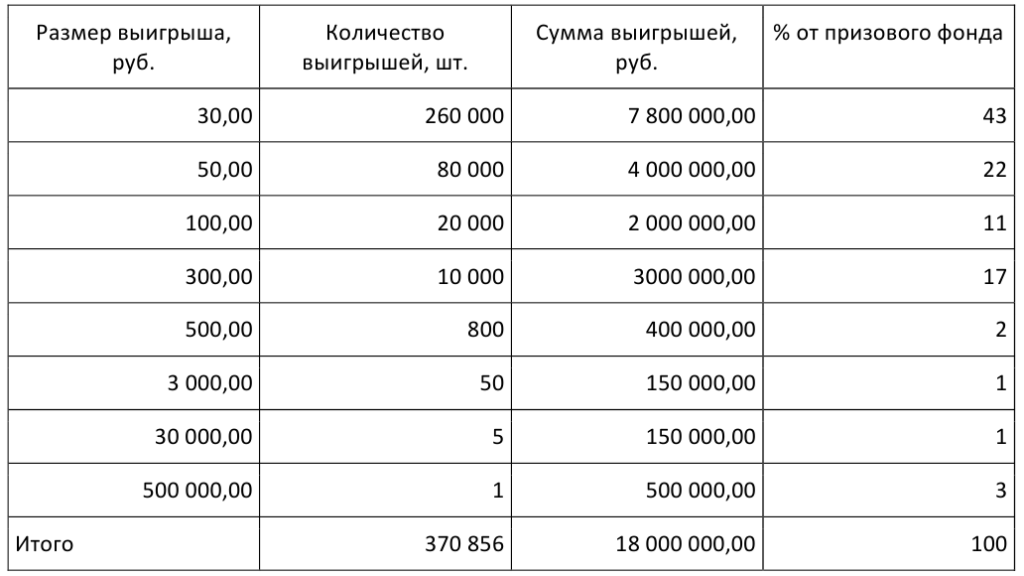
Sääntö 3. Tunne mahdollisuutesi
Jackpotin todennäköisyys missä tahansa arpajaisessa on, yleensä, yksi kaava. Ja tässä on todennäköisyyden laskeminen, esim, Ainakin yhden rivin sulkeminen lottossa on hyvin ei-triviaalia ja vie koko artikkelin, voi olla, eikä yksi. Siksi itse asiassa mahdollisuus saada rahaa arpajaisiin on suurempi johtuen siitä, että useimmilla arpajaisilla on lisäpalkintoja pääpalkinnon lisäksi. Mutta keskityn jättipottiin arvioinnin helpottamiseksi..
Tunnustetaan, ostimme arpalipun satunnaisilla numeroilla
Piirroksen aikana vedetään sama määrä palloja., ja jos niissä olevat numerot yhtyivät lipun numeroihin (missä tahansa järjestyksessä, on tärkeää!), sitten voitimme. Tällaisen voiton todennäköisyys lasketaan seuraavasti:
Yhdistelmien määrää ottamatta huomioon järjestystä kutsutaan matematiikassa yhdistelmien lukumääräksi, ja jos tiedät ja ymmärrät kaavan sen laskemiseksi, sitten tästä artikkelista, todennäköisesti, älä opi mitään uutta. Jos et ole matemaatikko, silloin verkkopalvelun käyttö on helpompaa, esimerkiksi tämän kanssa. Samankaltaiset palvelut (ja kaava, heidän työnsä taustalla) tarjous asettaa kaksi numeroa:
- n - yhden kohteen mahdollisten vaihtoehtojen kokonaismäärä. Meidän tapauksessamme esine on pallo, ja on niin paljon palloja, kuinka monta numeroa on arvonnassa, lisää tästä alla.
- k - kappaleiden määrä yhdessä näytteessä. Meidän tapauksessamme, kuinka monta palloa arpajaiset vetävät ja kuinka monta numeroa lipussa on (oletettu, että nämä määrät ovat samat).
niin, если у нас есть лотерея с розыгрышем 5 pallot, а всего в лотерее 50 шаров с числами от 1 että 50, silloin voiton todennäköisyys siinä on yhtä kuin k =: n yhdistelmien lukumäärä 5 ja n = 50, ts:
Harkitse monimutkaisempaa tapausta - suosittu amerikkalainen Powerball-arpajaiset, jossa jättipotin arvo ylitti miljardin dollarin. По правилам есть базовая выборка из 5 numerot (alkaen 1 että 69), ja myös yhden lisänumeron (alkaen 1 että 26). Нужно получить совпадение всех 6 numerot, voittaa.
Sitä ei ole vaikea ymmärtää, että mahdollisuus saada ensimmäinen sarja on yhtä kuin yksi yhdistelmien lukumäärästä k = 5 ja n = 69 (ts 11 238 513), ja mahdollisuus "kiinni" viimeinen pallo on 1 että 26. Saada kaikki kerralla, nämä mahdollisuudet on kerrottava, koska tapahtumien on tapahduttava samanaikaisesti:
Toisin sanoen, jos 300 миллионов человек купят билеты, silloin vain yksi voittaa. Se näyttää, miksi jättipottia ei usein voiteta ollenkaan: arpajaisten järjestäjät eivät vain tulosta niin monta lippua, niin että heidän joukossaan voittaa.