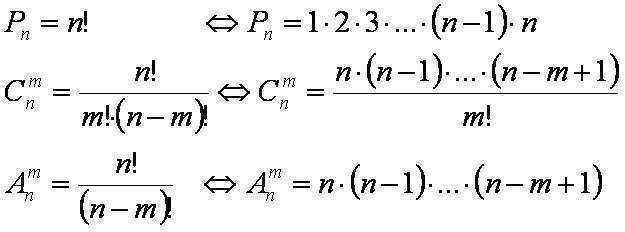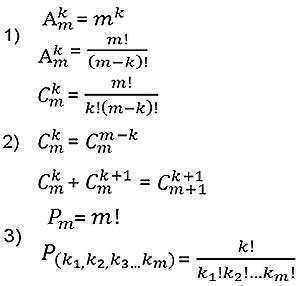Éléments combinatoires

La magie de l'argent en numérologie

Chaque nombre a sa propre énergie et affecte la vie d'une personne d'une certaine manière.. La numérologie de l'argent aide à déterminer la signification d'un nombre, découvrez le code personnel de l'argent et de la richesse. Le code fiscal est calculé en utilisant la date de naissance. Ensuite, vous devez voir la transcription. Vous devez également savoir, comment utiliser correctement votre code patrimonial.

L'essentiel est de calculer correctement le code financier

outre, quel est le nombre de richesses, il y a aussi des nombres, ne pas apporter l'abondance dans la vie d'une personne. Ils doivent être évités. Pour attirer les flux financiers, besoin de se familiariser avec, que signifie chaque nombre:

1. Zéro et un. Les numérologues croient, que ces nombres et codes sont négatifs pour l'énergie monétaire, ils ne porteront pas chance. Par conséquent, vous devez éviter les économies., dépôts avec montants, dans lequel ces nombres sont présents, car ils ralentiront les flux de trésorerie et n'apporteront ni prospérité ni succès.
2. Couple. C'est un chiffre malheureux. Elle n'apportera ni prospérité ni succès. Il n'est pas recommandé d'utiliser des billets de cette dénomination pour l'épargne, ne les portez pas dans votre portefeuille.
3. Trio. Est financièrement favorable, avec son aide, une personne peut gagner à la loterie, trouver des sources de revenus supplémentaires. Mais les numérologues ne recommandent pas d'accumuler des fonds., dont la somme est 300, 3000, 30000. Cette figure a besoin d'un mouvement constant, elle a besoin d'énergie, pas la paix. Le mieux est d'acheter un billet de loterie pour un tel montant ou de l'investir dans votre propre entreprise..
4. Les quatre dans le code personnel sont un symbole de stabilité, fiabilité. Idéal pour faire des économies, des économies, l'investissement est le montant des factures 400, 4000, 40000. De cette façon, la richesse augmentera.
5. Cinq est un code numérique très important de la richesse en numérologie. Les factures avec ce numéro sont des aimants en argent réel.. Ils peuvent être prêtés, dépenser en voyage, accumuler, dépenser ainsi, comme vous voulez.
6. Un tel code financier peut impliquer certaines contraintes financières.. Avec ce chiffre, les gens apprennent à épargner, contrôler vos dépenses. Les montants 600, 6000 sont un symbole de stabilité et de certitude. Les numérologues ne recommandent pas d'investir de tels montants.
7. Sept est le code, malchance, il ne peut pas être utilisé pour le stockage, investissements, des économies, les prêts et toutes autres transactions financières, qui sont associés au risque.
8. Huit est un code de richesse fort en numérologie, il est considéré comme très réussi. Dépôts pour montants 800, 8000, 80000 sont très réussis, ils attirent de l'argent, comme un aimant.
9. Neuf est un symbole de spiritualité et de développement intérieur. Amasser de l'argent avec ça n'arrivera pas, mais il n'y aura pas non plus de perte. Il est recommandé de dépenser des sommes avec un neuf sur l'auto-apprentissage, entraînement

Pour utiliser correctement les nombres, dois savoir, comment calculer le code de richesse. Ensuite, vous devez connaître les règles d'utilisation d'une telle combinaison.. Vais-je devenir riche, dépend non seulement du code obtenu à la suite du calcul, mais aussi de ça, comment l'utiliser correctement.

Informations de référence

Des documentsRapportspar mentions Base documentaire TitresDes provisionsDocuments financiersRésolutionsRubrique par thèmeFinanceVilles de la Fédération de Russierégionspar dates exactestermesTerminologie scientifique financière économiqueTempsDates 2015 2016 Documents dans le secteur financier dans l'investissement

Combinaisons sans répétitions

Une tâche: Trouvez toutes les combinaisons possibles sans répétitions à partir de nombreux éléments {1,2,3} par 2.
Les combinaisons suivantes existent:1: 1 22: 1 33: 2 3
Le nombre de combinaisons possibles sans répétitions de N éléments par M peut être déterminé par la formule (N≥M):

que dans M! fois moins que le nombre correspondant d'emplacements sans répétitions (car les combinaisons sans répétitions ne dépendent pas de l'ordre des éléments).
Considérons le problème de l'obtention de toutes les combinaisons pour les nombres 1 ... N par M. Implémentation en C ++

12345678910111213141516171819202122232425262728293031323334353637383940414243

#comprendre <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int k = m; pour (int i = k – 1; je >= 0; –je) si (une < n – k + je + 1) { ++une; pour (int j = i + 1; j < k; ++j) a = a + 1; return true; } retourner faux;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; pour (int i = 0; je < n; i++) cout << une << ” “; cout << endl;}int main() { int n, m, *une; cout << “N = “; cin >> n; cout << “M = “; cin >> m; a = new int; pour (int i = 0; je < n; i++) a = i + 1; Print(une, m); si (n >= m) { tandis que (SuivantSet(une, n, m)) Print(une, m); } cin.get(); cin.get(); revenir 0;}

Результат выполнения

Numérologie anglaise: concept et essence

Les plus anciennes connaissances, qui aident à expliquer, interpréter ça, ce que les anges veulent dire à l'homme, appelée numérologie angélique.

Rappel, que la numérologie étudie les vibrations des nombres, chiffres, leur influence sur les gens et leurs processus de vie. Un autre mathématicien anglais, l'astrologue John Dee au 16ème siècle a écrit un ouvrage sur les nombres, qu'il considérait comme la langue angélique universelle pour communiquer avec les gens.

La fondatrice de l'enseignement relativement jeune de la numérologie angélique est Doreen Verche. Clairvoyant d'Amérique, psychologue et philosophe, auteur de nombreux livres. Elle a dédié ses œuvres aux Êtres Suprêmes, y compris les dieux, anges, saints. Depuis de nombreuses années, elle étudie des phénomènes inexpliqués.. Mais ça en valait la peine. Elle a créé l'instrument, qui peut vous aider à interpréter les messages de vos assistants du ciel. Selon Doreen Verce, nous recevons régulièrement des signes des anges, qui avertissent des dangers, suggérer des solutions aux problèmes de la vie d'une personne.

Les anges parlent à l'homme en chiffres, des lettres, panneaux. Les œuvres de Doreen Verce parlent d'indices de gardiens invisibles, qui sont codés dans des chiffres répétés ou des combinaisons de ceux-ci. À savoir:

• sur les plaques d'immatriculation des voitures;
• sur l'horloge;
• dans le brownie, appartement, numérotation des bureaux;
• en dates de naissance;
• sous forme de ticket, comme dans les transports, et installations publiques, etc..

Dans toutes ces combinaisons, les chiffres masquent les données, qui peut faire des ajustements à l'avenir des gens. Doreen Verce a fait beaucoup de recherches sur le sujet, dédié aux calculs numérologiques par date de naissance. De tels calculs aident à identifier les enfants., qui ont des capacités uniques depuis la naissance, et pas seulement.

Nombre de correspondances, combinaisons que nous ne remarquons souvent pas

Mais ça vaut la peine de prêter attention à, car un tel phénomène peut être un avertissement important. Après tout, les anges ne nous envoient pas un tel signe pour rien

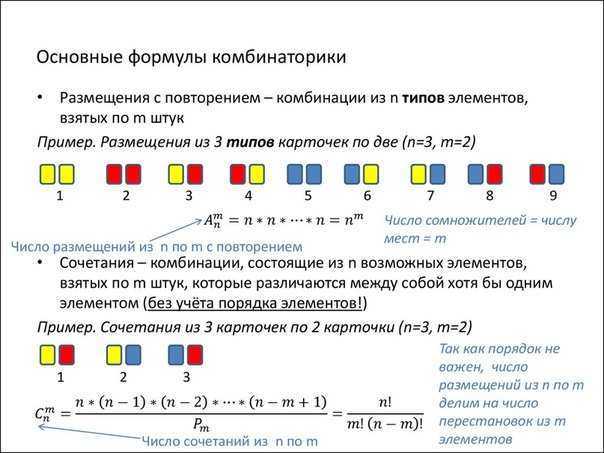
Combinaisons avec répétitions

Les combinaisons avec des répétitions sont des ensembles de M éléments, auquel chaque élément de l'ensemble N peut participer plusieurs fois. Dans ce cas, aucune restriction n'est imposée sur le rapport des valeurs de M et N, et le nombre total de combinaisons avec des répétitions est

Un exemple d'un tel problème est le choix de M cartes postales parmi N de toutes les manières possibles.

Pour générer des combinaisons avec des répétitions, nous utiliserons la solution de génération d'emplacements avec des répétitions., considéré. Implémentation C ++

1234567891011121314151617181920212223242526272829303132333435363738394041

#comprendre <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int j = m – 1; tandis que (a == n && j >= 0) j–; si (j < 0) retourner faux; si (une >= n) j–; a++; si (j == m – 1) return true; pour (int k = j + 1; k < m; k++) a = a; return true;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; pour (int i = 0; je < n; i++) cout << une << ” “; cout << endl;}int main() { int n, m, *une; cout << “N = “; cin >> n; cout << “M = “; cin >> m; int h = n > m ? n : m; // размер массива а выбирается как max(n,m) a = new int; pour (int i = 0; je < h; i++) a = 1; Print(une, m); tandis que (SuivantSet(une, n, m)) Print(une, m); cin.get(); cin.get(); revenir 0;}

Le résultat de l'algorithme ci-dessus:

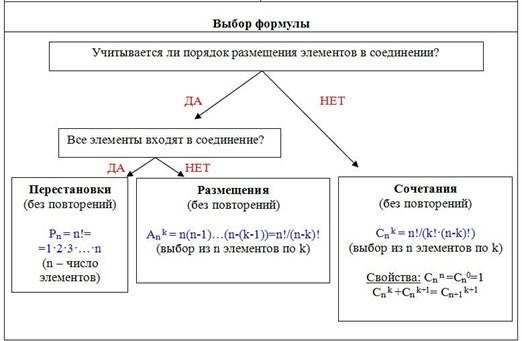
Algorithmisation

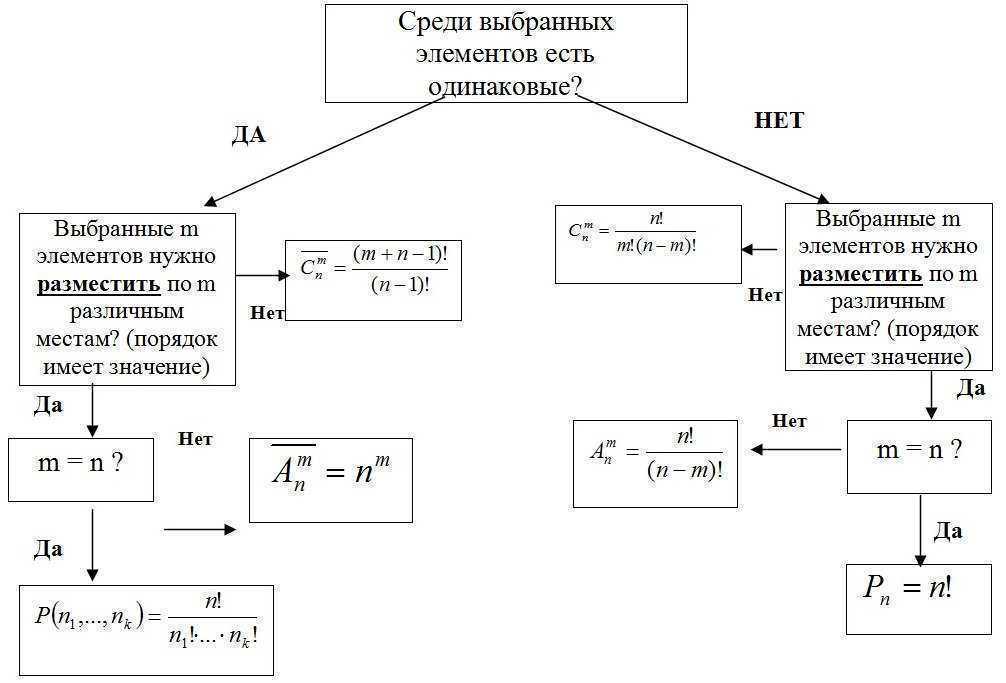
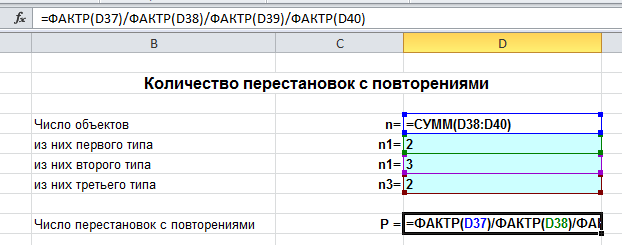
La formule de base de la combinatoire

Soit k groupes d'éléments, et le i-ème groupe se compose de n_je éléments.
Sélectionnez un élément de chaque groupe. Puis le nombre total N de voies,
avec lequel un tel choix peut être fait, est défini par la relation N = n₁*n₂*n₃*…*n_k.

Exemple 1. Expliquons cette règle dans un simple
exemple. Qu'il y ait deux groupes d'éléments, et le premier groupe se compose de
n₁ éléments, et le deuxième – de n₂ éléments. combien
différentes paires d'éléments peuvent être composées de ces deux groupes, de cette façon,
afin qu'il y ait un élément dans une paire de chaque groupe? Admettons, Nous avons pris
le premier élément du premier groupe et, sans le changer, allé sur tout possible
des couples, modifier uniquement les éléments du deuxième groupe. De telles paires pour cet élément
peut être n₂. Ensuite, nous prenons le deuxième élément du premier groupe
et composez également toutes les paires possibles pour cela. Il y aura également n paires de ce type₂.
Puisque le premier groupe ne contient que n₁ élément, tout est possible
les options seront n₁*n₂.Exemple 2. combien
les nombres pairs à trois chiffres peuvent être composés de chiffres 0, 1, 2, 3, 4, 5, 6, si
les nombres peuvent être répétés?Décision: n₁= 6
(car. comme premier chiffre, vous pouvez prendre n'importe quel chiffre de 1, 2, 3, 4, 5, 6), n₂= 7
(car. comme deuxième chiffre, vous pouvez prendre n'importe quel chiffre de 0, 1, 2, 3, 4, 5,
6), n₃= 4 (car. comme troisième chiffre, vous pouvez prendre n'importe quel chiffre de 0, 2, 4,
6).

alors, N = n₁*n₂*n₃= 6 * 7 * 4 = 168.

Dans ce cas, lorsque tous les groupes ont le même nombre d'éléments, c'est à dire. n₁= n₂=…n_k= n
cela pourrait être considéré, que chaque choix est fait du même groupe, de plus
l'élément après la sélection retourne au groupe. Puis le nombre de toutes les manières
le choix est nk. Ce type de sélection en combinatoire est appelé sélection avec retour.

Exemple 3. Combien sont tous des nombres à quatre chiffres
peut être composé de nombres 1, 5, 6, 7, 8?Décision. Pour chaque rang
un nombre à quatre chiffres il y a cinq possibilités, signifie N = 5 * 5 * 5 * 5 = 54 = 625.

Considérez l'ensemble, composé de n éléments. il
un ensemble en combinatoire est appelé général
agrégat.

Affaires et finance

BanquesSanté et bien-êtreCorruption(la criminalité)MarketingGestionInvestissementsSécuritéGestionSociétés publiques par actionsProjetsDocumentsSécurité – contrôler les titres – Évaluation Obligations Dettes Monnaie Immobilier(Location)ProfessionsEmploisTradingServicesFinanceAssuranceBudgetServices financiers

Que faire avec le code mantrique après avoir terminé le rituel

Après, comment les valeurs numériques ont été lues pendant 77 journées, ils devraient être accusés de 4 éléments pour un travail ultérieur.

Pour ce faire, vous devez effectuer des manipulations simples.:

1. Activez le code avec l'énergie de la Terre. Un petit pot de terre convient au rituel.. Vous aurez également besoin de graines de fleurs. Ce devraient être exactement les graines., pas les pousses et les tubercules des plantes. Après avoir préparé les attributs requis, le mantra doit être écrit sur un morceau de papier vierge et enterré dans le sol, dire les mots trois fois - «La terre est pleine de richesses, tu es maintenant mon rêve ». Ensuite, une graine de fleur est placée dans le pot.
2. Après l'élément Terre, le mantra est chargé de l'énergie de l'eau. Ce rituel consiste à arroser la graine, qui est accompagné des mots «Eau et terre, raviver les graines ». Comme dans le cas précédent, faire une déclaration 3 fois.
3. Vient ensuite le tour des éléments de l'Air. Le pot avec la future plante doit être amené à une fenêtre ouverte et dit: "Toi, Air, j'ai besoin de, comme la lumière, et donne mon rêve Dawn ". Il doit être répété dans 3 journées.
4. Quand une graine apparaît, il est temps pour les éléments du feu. Une nouvelle bougie allumée est nécessaire pour réveiller le mantra. Il doit être placé à côté de la plante et, se concentrer, dis trois fois: "Ça brûle, Feu, bougie - brûler, et détruire la pauvreté. Laisse pousser la pousse, que cache l'argent. Et je vais m'épanouir avec lui, attirer la richesse en argent ".

Après ces étapes, le code de devise commence à fonctionner. Il est conseillé de ne pas jeter le pot avec la pousse et le mantra, poursuivre les soins habituels de la plante.

outre, pour améliorer l'effet du code mantrique, vous pouvez appliquer l'image de nombres sur une feuille de carton à l'aide d'encre verte et rouge. Un tel talisman d'argent doit être constamment emporté avec vous..

La magie des choses familières

Notre générateur de nombres aléatoires en ligne.

Notre générateur de randomisation ne nécessite pas de le télécharger sur votre PC personnel. Tout se passe en mode générateur de nombres en ligne. Spécifiez simplement ces paramètres, comme: plage de nombres en ligne, dans lequel les nombres seront choisis au hasard. Indiquez également le nombre de chiffres, qui sera choisi.
Par exemple, у Вас есть группа Вконтакте. В группе вы разыгрываете 5 prix, parmi les participants, qui republiera le disque. Utiliser une application dédiée, nous avons une liste de participants. Chacun a reçu un numéro séquentiel pour les numéros en ligne.

Allez maintenant sur notre générateur en ligne et spécifiez la plage de nombres (nombre de participants). par exemple, demander, de quels numéros en ligne ont besoin 5, depuis que nous avons 5 prix. Теперь жмем кнопку генерации. Ensuite, nous obtenons 5 nombres aléatoires en ligne, allant de 1 à 112 compris. Généré 5 les numéros en ligne correspondront au numéro de série de cinq participants, qui sont devenus les gagnants du dessin. Tout est simple et pratique.

Un autre avantage du générateur de nombres aléatoires est, que tous les numéros en ligne sont donnés au hasard. C'est-à-dire pour l'influencer, ou calculer, quel numéro sera le prochain, ne semble pas possible. Ce que fait le générateur peut être dit, honnête et fiable, et l'administration, quels prix tirez au sort en utilisant notre générateur gratuit, honnête et décent face aux participants du concours. Et si vous avez un doute sur une solution, alors vous pouvez utiliser notre générateur de réponse oui ou non.

Comment calculer votre code patrimonial

Il y a de bonnes et de mauvaises combinaisons

La numérologie et l'argent sont étroitement liés. Il existe des combinaisons de nombres, générateur de richesse, mais il y a des combinaisons infructueuses. Si vous les appliquez correctement, le succès et la chance seront de votre côté. Le calcul du code est simple. Pour ce faire, vous devez effectuer les calculs suivants:

• écrivez votre numéro sur une feuille de papier vierge, mois et année de naissance (par exemple, 31.10.1987);
• pour calculer la valeur de succès, les deux premiers chiffres doivent être ajoutés, c'est à dire, date de naissance précise (par exemple, 31 - 3 + 1 = 4). Ce numéro sera le premier de la combinaison;
• pour calculer le deuxième caractère de la combinaison, il faut calculer la valeur du mois (par exemple, octobre, 10 mois - 1 + 0 = 1);
• maintenant vous devez calculer le montant de l'année de naissance (par exemple, 1987 - 1 + 9 + 8 + 7 = 25, 2+5= 7);
• à la fin, vous devez calculer personnellement le dernier caractère de la combinaison, pour cela, les trois numéros reçus précédents sont résumés (par exemple, 4+1+7= 12, 1+2= 3, dans ce cas, la combinaison d'argent est 4173). La combinaison résultante est un code personnel pour une personne..

En plus du code personnel, il y a des valeurs universelles, que tout le monde peut postuler, comme un millionnaire, et à revenu moyen. C'est une mascotte numérique, qui est représenté sous la forme de quatre huit de taille égale. Cette combinaison est très forte, signifie succès monétaire et stabilité.

Vous pouvez également calculer ensuite, vais-je être riche, de nom. Pour cela, un tableau de correspondance entre les lettres et les chiffres est pris. Par exemple, Marina, qui est né 5 Nombres. Dans ce cas, seul l'anniversaire est pris:

M-5, A-1, R-9, I-1, N-6, A-1. 5+1+9+1+6+1= 23, 2+3= 5. Ensuite, ajoutez la date de naissance - 5 + 5 = 10, 1+0= 1 - un et est le code de la chance et de l'argent pour une personne spécifique. Mais peut-il réussir, dépend de, comment il est utilisé.

Permutations de n éléments

Définition 3. Permutation
de n éléments
tout ensemble ordonné est appelé
ces éléments.

Exemple 7a. Toutes sortes de permutations
multitudes, composé de trois éléments {1, 2, 3} sont: (1, 2, 3), (1, 3,
2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

Le nombre de permutations distinctes de n éléments est noté P_n et
est calculé par la formule P_n= n!.

Exemple 8. De combien de manières sept livres
différents auteurs peuvent être disposés sur une rangée sur l'étagère?Décision:ce problème sur le nombre
réorganiser sept livres différents. Il y a P₇= 7!= 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040
façons d'organiser des livres.

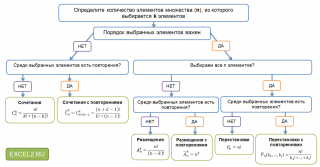
Discussion. Nous voyons,
que le nombre de combinaisons possibles peut être calculé selon différentes règles
(permutations, combinaisons, placement) et le résultat sera différent,
car. le principe du comptage et les formules elles-mêmes sont différentes. Regardant de près
définitions, peut être vu, que le résultat dépend de plusieurs facteurs
à la fois.
En premier, à partir de ce, à partir de combien d'éléments pouvons-nous les combiner
ensembles (quelle est la taille de la population totale d'éléments).
Deuxièmement, le résultat dépend de, quelle est la taille des ensembles d'éléments pour nous
avoir besoin

Et le dernier, c'est important de savoir, est pour nous
ordre essentiel des articles dans un ensemble. Expliquons le dernier facteur sur
exemple suivant

Exemple 9. À la réunion des parents
présent 20 homme. Combien d'options de composition différentes existe-t-il
comité de parents, s'il doit entrer 5 homme?Décision: Dans cet exemple, nous
pas intéressé par l'ordre des noms dans la liste des comités. Si, en conséquence, dans son
la composition sera les mêmes personnes, alors le sens pour nous est le même
option. Par conséquent, nous pouvons utiliser la formule pour calculer le nombre de combinaisons à partir de 20 éléments par 5.
Les choses seront différentes, si chaque membre du comité est initialement responsable
direction définitive du travail. Puis avec la même paie
Comité, à l'intérieur c'est possible 5! options de permutation, quelle importance. nombre
différent (et composition, et par domaine de responsabilité) options définies dans
dans ce cas, le nombre d'emplacements
de 20 éléments par 5.

Tâches d'autotest
1. Combien de nombres pairs à trois chiffres peuvent être créés à partir de chiffres 0, 1, 2, 3, 4, 5,
6, si les nombres peuvent être répétés?
Depuis. un nombre pair à la troisième place peut être 0, 2, 4, 6, c'est à dire. Quatre chiffres. N'importe lequel des sept chiffres peut être à la deuxième place. En premier lieu, il peut s'agir de l'un des sept chiffres sauf zéro, c'est à dire. 6 Opportunités. Résultat = 4 * 7 * 6 = 168.
2. Combien de nombres à cinq chiffres y a-t-il, qui lit la même chose sur la gauche
droite et droite à gauche?
N'importe quel nombre peut être en premier lieu sauf 0, c'est à dire. 9 Opportunités. N'importe quel nombre peut être à la deuxième place, c'est à dire. 10 Opportunités. N'importe quel nombre de, c'est à dire. 10 Opportunités. Les quatrième et cinquième chiffres sont prédéfinis, ils correspondent au premier et au second, Par conséquent, le nombre de ces nombres est 9 * 10 * 10 = 900.
3. Il y a dix matières et cinq leçons par jour dans la classe. De bien des façons, vous pouvez
faire un programme pour une journée?
4. Combien de façons vous pouvez choisir 4 délégué à la conférence, si dans un groupe
20 homme?

n = C₂₀4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)= 4845.

5. De combien de façons huit lettres différentes peuvent-elles être décomposées en huit
diverses enveloppes, si une seule lettre est mise dans chaque enveloppe?
Vous pouvez mettre la première enveloppe 1 de huit lettres, dans le second des sept restants, dans le troisième de six etc.. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Trois mathématiciens et dix économistes doivent être composés d'une commission,
composé de deux mathématiciens et six économistes. Combien de façons est-ce
peut être fait?

Nombre de façons de choisir math C₃2= 3!/(2!*(3-2))!= 3/2, nombre de façons de choisir l'économiste C₁₀6= 10!/(6!*(10-6))!= 7 * 8 * 9 * 10 /(1*2*3*4)= 210. n = C₃2*DE₁₀6= 3 * 210 = 630.