A szabály 4. Indítsa el időben
PowerBall sorsjegy, Apropó, érdemes 2 dollár. Az előnyök kiszámításához, ami megtérítené a jegy megvásárlását, нужно умножить цену билета на 292 201 338.
További információ a számításokról. Ez utalás az első pontra., ahol azt mondja, hogy egy megoldás előnye megegyezik annak értékével, szorozva a valószínűséggel. Ha 1 / X valószínűségű és N értékű eseményünk van, akkor a haszon N / X lesz. Мы тратим 2 доллара и можем подсчитать, mennyit fizetne meg a győzelem a jegyvásárlásnál:
- 2 = N ÷ X.
- N = 2 × X, а X тут как раз равен 292 201 338, amint azt az előző rész számításai mutatják.
Figyelembe kell vennie az adókat is (felfedez, a bevallott összeg hány százaléka kerül valójában a nyertesre, általában kb 70%). То есть джекпот должен составлять как минимум 850 millió dollár, és ez ebben a lottón történik. Hogy hogy, - mondtam az elején, hogy az ilyen szorzásban rejlő nyereség mindig nem a játékos javát szolgálja?
Ami azt illeti, mi van, ha a jackpotot nem sorsolták ki, aztán legközelebb megy, és ezért a pénz egy ideig felhalmozódik, és folytatódik a jegyértékesítés.
De lehetetlen előre megtudni. Elkezdheti azonban a jegyek vásárlását, amint a jackpot mérete meghaladja az említett összeget. Ilyen helyzetben matematikailag előnyös lesz a játék.
Még mindig megértheti, ami jövedelmezőbb: vásároljon sok jegyet egy játékra, vagy vegyen egy jegyet sok játékra? Gondolkozzunk.
A valószínűségelméletben létezik a nem kapcsolódó események fogalma. Azt jelenti, hogy az egyik esemény kimenetele nem befolyásolja a másik kimenetelét. például, ha két kockát dobsz, akkor a rajtuk eső számok nem kapcsolódnak egymáshoz: a véletlenszerűség szempontjából, az egyik kocka nem befolyásolja a másik viselkedését. De ha kihúz két kártyát a pakliból, akkor ezek az események összekapcsolódnak, mert az első kártya attól függ, milyen kártyák maradnak a pakliban.
Az ezzel kapcsolatos népszerű tévhitet játékos hibának nevezzük.. Az ember intuitív elképzeléséből fakad a nem kapcsolódó események összekapcsoltságáról.
Visszatérve a lottóhoz: a különböző játékok nem összefüggő események, mert a gömbök sorrendjét újból kiválasztják. Tehát egy adott lottó megnyerésének esélye nem attól függ, hogy, hányszor játszottad már korábban. Nagyon nehéz intuitív módon elfogadni., mert egy személy minden alkalommal, jegyet vásárol, azt hiszi: - Nos, most szerencséd van, meddig, Sokat játszottam!" De nem, a valószínűségelmélet szívtelen dolog.
De ha több játékot vásárolsz egy játékra, arányosan nő az esélyed, mert az egyik játék belsejében jegyek kötöttek: ha valaki nyer, eszközök, Egyéb (egy másik kombinációval) biztosan nem fog nyerni. Покупка 10 билетов увеличивает шансы в 10 idő, ha a jegyeken szereplő összes kombináció eltér (valójában szinte mindig az). Más szavakkal, если у вас есть деньги на 10 jegyek, jobb, ha megveszed őket egy játékra, чем покупать по билету на 10 játékok.
Ha csak havonta egyszer veszel jegyet a fizetésedből a kedvéért, akkor, valószínűleg, a játék folyamata számít neked. Математически выгоднее скопить эти деньги и в конце года купить сразу 12 jegyek, habár, természetesen, egy ilyen helyzetben bekövetkező veszteség pusztítóbb lesz.
A szabály 1. Értékelje a kockázatokat
Nem titok egy modern felvilágosult ember számára, hogy a kaszinók és a különféle szerencsejáték-létesítmények minden játékukat úgy számolják, hogy mindig győztes legyek és profitot termeljek. Ez nagyon egyszerűen történik: az illetőnek vissza kell adnia a nyereményt, ami korrelál a tétjének csökkenésével a nyerési esélyeihez képest.
Nincsenek kivételek, kivéve, ha valaki kifejezetten pénzt akar adni. Tartsa szem előtt ezt az egyszerű szabályt, hogy mindig józanul nézzünk a helyzetre.
A játékelmélet ugyanúgy értékel minden stratégiát: a győzelem megszerzésének valószínűségét megszorozzuk a méretével. Durván mondva, a matematika számít, что гарантированно получить 1 000 рублей — это как получить 2 000 рублей с 50-процентным шансом. Ez az elv lehetőséget ad arra, hogy nagyjából összehasonlítsa a különböző játékokat egymással.. Mi a jobb: миллион долларов с шансом 1/100 000 vagy 50 долларов с шансом 1/4? Intuitívnak tűnik, hogy az első mondat érdekesebb, de ez utóbbi matematikailag előnyösebb.
Ha egyedül marad a matematika keretein belül, kiszámítható: lehetetlen nyerni a kaszinóban, mert bármely választott stratégia oda vezet, hogy a nyerési valószínűség szorzata a játékos fizetésének nagysága alapján mindig alacsonyabb, mint a tét, amit már megtett.
És azért is, hogy a pénz nemlineáris számunkra: формально получить 1 рубль прямо сейчас — это как получить миллион рублей с шансом 1/1 000 000, de valójában a rubel elvesztése semmilyen módon nem befolyásolja állapotunkat, semmi nem fog változni az életben, de millió megszerzése nagyon komoly esemény.


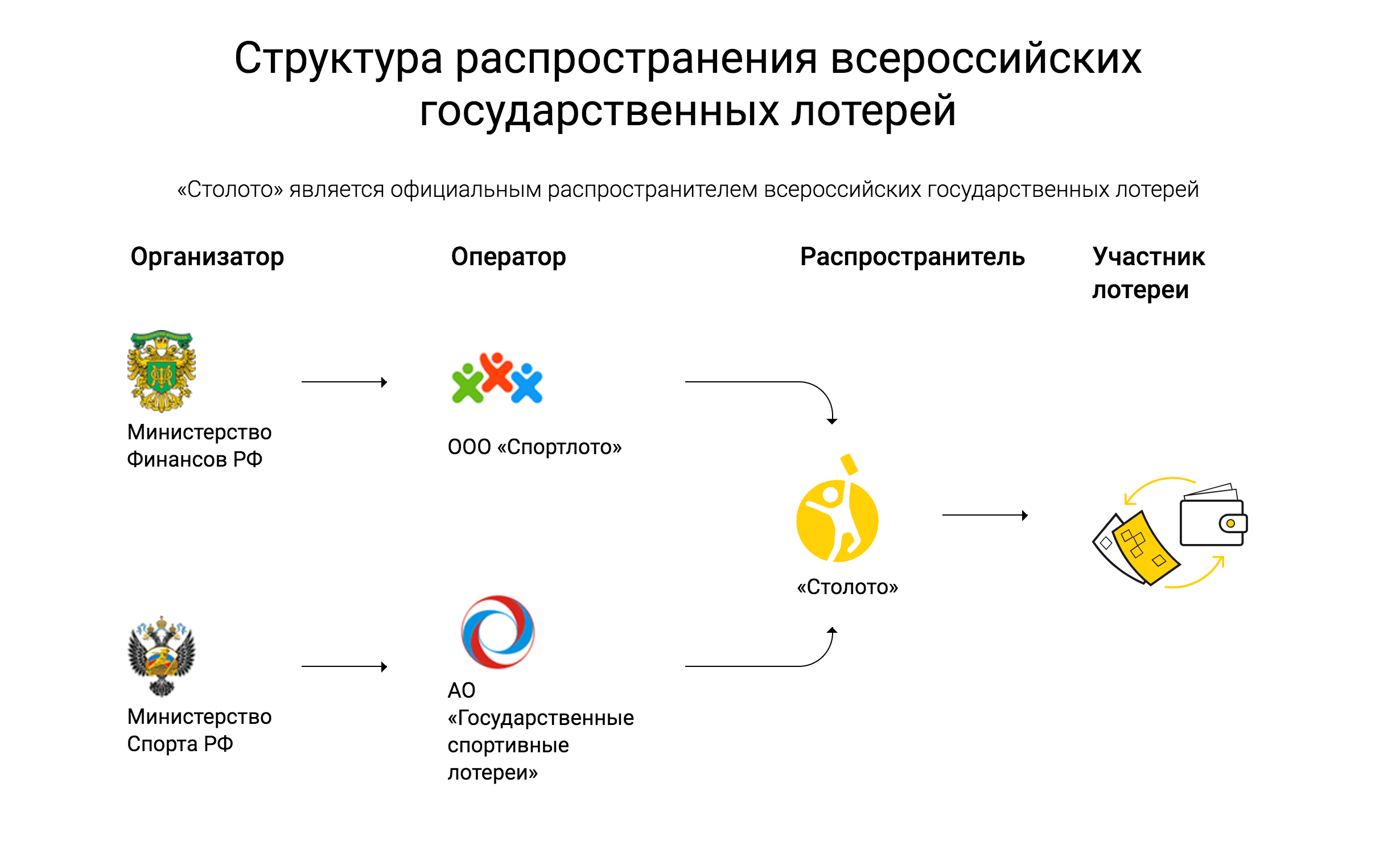
![Oroszország legjobb 15 lottója, amelyben nyerni lehet [csalás nélkül]](https://ivaquest.ru/wp-content/uploads/f/3/5/f35c05b06576e149ae818909943200c0.jpg)