Какая лотерея самая лучшая

Правило 4. Вовремя начинайте

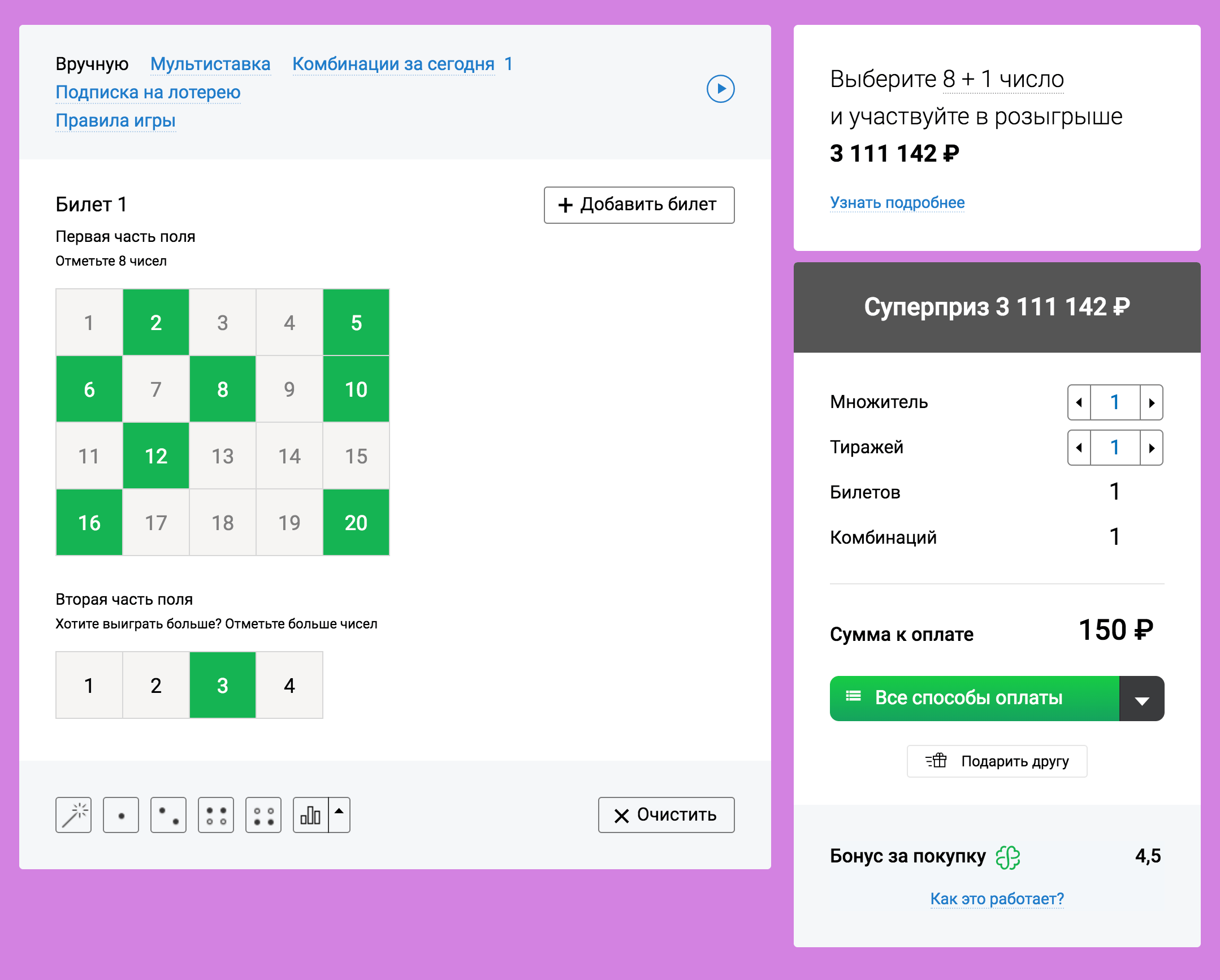
Лотерейный билет PowerBall, кстати, стоит 2 доллара. Чтобы подсчитать выгоду, которая окупила бы покупку билета, нужно умножить цену билета на 292 201 338.

Подробнее о расчётах. Это отсылка к первому пункту, где говорится о том, что выгода от решения равна его ценности, умноженной на вероятность. Если у нас есть событие с вероятностью 1/X и ценностью N, то выгода будет N/X. Мы тратим 2 доллара и можем подсчитать, какого размера выигрыш окупил бы покупку билета:

• 2 = N ÷ X.
• N = 2 × X, а X тут как раз равен 292 201 338, как показали расчёты из предыдущей части.

Ещё надо учесть налоги (узнать, какой процент от заявленной суммы фактически достанется победителю, обычно это около 70%). То есть джекпот должен составлять как минимум 850 миллионов долларов, и такое в этой лотерее бывает. Как же так, я ведь в начале сказал, что выигрыш при таком умножении всегда не в пользу игрока?

Дело в том, что если розыгрыш джекпота не состоялся, то он переходит на следующий раз, и поэтому какое-то время деньги копятся, а продажи билетов продолжаются.

Но узнать это заранее невозможно. Однако можно начать покупать билеты, как только размер джекпота станет больше упомянутой суммы. В такой ситуации математически игра будет выгодной.

Ещё можно понять, что выгоднее: купить много билетов на одну игру или покупать по одному билету на много игр? Давайте подумаем.

В теории вероятностей есть понятие несвязанных событий. Это означает, что исход одного события никак не влияет на исход другого. Например, если вы кидаете два кубика, то выпадения чисел на них не связаны между собой: с точки зрения случайности, один кубик не влияет на поведение второго. А вот если вы тянете из колоды две карты, то эти события связаны, ведь от первой карты зависит то, какие карты останутся в колоде.

Популярное заблуждение по этому поводу так и называется — ошибка игрока. Оно возникает из-за интуитивного представления человека о связанности несвязанных событий.

Возвращаясь к лотереям: разные игры — это несвязанные события, потому что последовательность шаров выбирается заново. Так что шансы выиграть в любую конкретную лотерею никак не зависят от того, сколько раз раньше вы в неё играли. Это очень сложно принять интуитивно, потому что человек каждый раз, покупая билет, думает: «Ну вот сейчас-то повезёт, сколько можно, я уже кучу времени играю!» Но нет, теория вероятностей — бессердечная штука.

А вот покупка нескольких билетов для одной игры увеличивает ваши шансы пропорционально, потому что билеты внутри одной игры связаны: если выиграет один, значит, другой (с другой комбинацией) точно не выиграет. Покупка 10 билетов увеличивает шансы в 10 раз, если все комбинации на билетах разные (по факту почти всегда так и есть). Иными словами, если у вас есть деньги на 10 билетов, лучше купить их на одну игру, чем покупать по билету на 10 игр.

Если вы просто с зарплаты раз в месяц берёте билетик азарта ради, то, скорее всего, значение для вас имеет сам процесс игры. Математически выгоднее скопить эти деньги и в конце года купить сразу 12 билетов, хотя, конечно, проигрыш в такой ситуации будет восприниматься более сокрушительно.

Правило 1. Оценивайте риски

Для современного просвещённого человека не секрет, что казино и различные игорные заведения рассчитывают все свои игры так, чтобы всегда быть в выигрыше и иметь прибыль. Делается это очень просто: человеку нужно вернуть выигрыш, который соотносится с его ставкой в меньшую сторону по сравнению с его шансами выиграть.

Исключений нет, если только кто-то специально не хочет подарить вам денег. Держите в голове это простое правило, чтобы всегда трезво смотреть на ситуацию.

Теория игр оценивает любую стратегию аналогично: вероятность получить выигрыш умножается на его размер. Грубо говоря, математика считает, что гарантированно получить 1 000 рублей — это как получить 2 000 рублей с 50-процентным шансом. Этот принцип даёт вам возможность грубо сравнивать различные игры между собой. Что лучше: миллион долларов с шансом 1/100 000 или 50 долларов с шансом 1/4? Интуитивно кажется, что первое предложение интереснее, но математически выгоднее второе.

Если оставаться в рамках одной лишь математики, можно вычислить: выиграть в казино невозможно, ведь любая выбранная стратегия приводит к тому, что произведение вероятности победы на размер выплаты для игрока всегда ниже ставки, которую он уже сделал.

А ещё потому, что деньги для нас нелинейны: формально получить 1 рубль прямо сейчас — это как получить миллион рублей с шансом 1/1 000 000, но по факту потеря рубля никак не скажется на нашем состоянии, в жизни не изменится совершенно ничего, а вот получение миллиона — очень серьёзное событие.