Секреты от лотерейных миллионеров
Самым популярным лотерейным миллионером стал Ричард Ластинг, который сумел 7 раз победить и получить денежный приз. Во время игры он использовал следующую инструкцию:
- Все числа не должны находиться по соседству.
- Чем больше количество билетов, тем выше шансы на победу. Ричард покупал не меньше 20 штук каждый розыгрыш.
- Быть готовым к расходам в случае проигрыша., подсчитывать убытки.
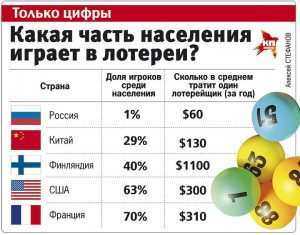
- Чем популярнее лотерея, тем меньше шансов на успех. При большом количестве участников сумма выигрыша существенно уменьшается.
- Сумму выбранных чисел необходимо высчитывать, она должна находиться в диапазоне от 104 до 172.
- Всегда использовать одну и ту же последовательность чисел. Случайные комбинации могут оказываться проигрышными.
- Покупать билеты на все розыгрыши.
Ни одна методика не даст гарантии, как купить билет, который принесет удачу. Повезти может каждому. В любом случае чтобы стать победителем необходимо приобрести лотерейный билет. Беспроигрышных лотерей не бывает.
Правило 3. Знайте свои шансы
Вероятность джекпота в любой лотерее считается, как правило, одной формулой. А вот расчёт вероятности, например, закрыть в лото хоть одну строчку весьма нетривиален и занял бы целую статью, а может, и не одну. Поэтому на самом деле шанс получить какие-то деньги в лотерее выше за счёт того, что в большинстве лотерей есть дополнительные призы помимо главного. Но я остановлюсь именно на джекпоте для простоты оценки.
Допустим, мы купили лотерейный билет со случайным набором чисел
Во время розыгрыша вытаскивают столько же шаров, и если числа на них совпали с числами в билете (в любом порядке, это важно!), то мы выиграли. Вероятность такого выигрыша рассчитывается так:
Количество комбинаций без учёта порядка называется в математике числом сочетаний, и если формула для его расчёта вам известна и понятна, то из этой статьи вы, скорее всего, не узнаете ничего нового. Если вы не математик, то проще будет воспользоваться онлайн-сервисом, например вот этим. Подобные сервисы (и формула, лежащая в основе их работы) предлагают задать два числа:
- n — общее количество возможных вариантов одного предмета. В нашем случае предмет — это шар, а всего шаров столько, сколько чисел в лотерее, об этом ниже.
- k — количество предметов в одной выборке. В нашем случае — сколько шаров лотерея разыгрывает и сколько при этом чисел в билете (предполагается, что эти величины равны).
Итак, если у нас есть лотерея с розыгрышем 5 шаров, а всего в лотерее 50 шаров с числами от 1 до 50, то вероятность выиграть в неё будет равна единице к числу сочетаний при k = 5 и n = 50, то есть:
Рассмотрим более сложный случай — популярную американскую лотерею PowerBall, в которой величина джекпота превышала миллиард долларов. По правилам есть базовая выборка из 5 чисел (от 1 до 69), а также одно дополнительное число (от 1 до 26). Нужно получить совпадение всех 6 чисел, чтобы выиграть.
Несложно понять, что шанс получить первый набор равен единице к числу сочетаний при k = 5 и n = 69 (то есть 11 238 513), а шанс «поймать» последний шар — 1 к 26. Чтобы получить всё сразу, эти шансы нужно умножить, потому что события должны произойти одновременно:
Иными словами, если 300 миллионов человек купят билеты, то выиграет кто-то один. Это показывает, почему выигрыш джекпота зачастую вообще не состоится: организаторы лотереи просто не печатают так много билетов, чтобы среди них попался выигрышный.