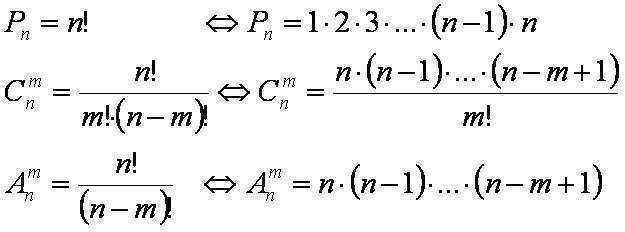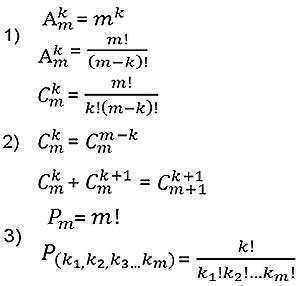Kombinatoriske elementer

Magien med penger i numerologi

Hvert tall har sin egen energi og påvirker en persons liv på en bestemt måte.. Numerologi med penger hjelper til med å bestemme betydningen av et tall, finne ut den personlige koden for penger og formue. Skattekoden beregnes med fødselsdato. Da må du se transkripsjonen. Du må også vite, hvordan du bruker formuekoden riktig.

Det viktigste er å beregne finanskoden riktig

I tillegg, hva er antall velstand?, det er også tall, ikke gir overflod til en persons liv. De må unngås. Å tiltrekke seg økonomisk flyt, trenger å bli kjent med, hva står hvert tall for:

1. Null og ett. Numerologer tror, at disse tallene og kodene er negative for monetær energi, de gir ikke lykke til. Derfor bør du unngå besparelser., innskudd med beløp, der disse tallene er til stede, fordi de vil redusere kontantstrømmen og ikke vil gi velstand og suksess.
2. Par. Dette er en uheldig figur. Hun vil ikke bringe velstand og suksess. Det anbefales ikke å bruke sedler fra denne betegnelsen til sparing, ikke ha dem i lommeboken.
3. Trekant. Er økonomisk gunstig, med sin hjelp kan en person vinne i lotteriet, finne flere inntektskilder. Men numerologer anbefaler ikke å samle inn penger., summen av det er 300, 3000, 30000. Denne figuren trenger konstant bevegelse, hun trenger energi, ikke fred. Det beste er å kjøpe lodd for et slikt beløp eller investere det i din egen virksomhet..
4. De fire i personlig kode er et symbol på stabilitet, pålitelighet. Ideell for besparelser, besparelser, investering er mengden regninger 400, 4000, 40000. På denne måten, rikdom vil øke.
5. Fem er en veldig viktig numerisk rikdomskode innen numerologi. Regninger med dette tallet er magneter med ekte penger.. De kan lånes ut, bruke på reise, akkumulere, bruke det, som du liker.
6. En slik finansiell kode kan medføre visse økonomiske begrensninger.. Med denne figuren lærer folk å spare, kontrollere utgiftene dine. Beløp 600, 6000 er et symbol på stabilitet og sikkerhet. Numerologer anbefaler ikke å investere slike beløp.
7. Seven er kode, uflaks, den kan ikke brukes til lagring, investeringer, besparelser, lån og andre finansielle transaksjoner, som er forbundet med risiko.
8. Åtte er en sterk formueskode innen numerologi, han regnes som veldig vellykket. Innskudd for beløp 800, 8000, 80000 er veldig vellykkede, de tiltrekker seg penger, som en magnet.
9. Ni er et symbol på åndelighet og indre utvikling. Å skaffe penger med det vil ikke skje, men det blir ikke noe tap heller. Det anbefales å bruke summer med en ni på selvstudium, opplæring

Å bruke tall riktig, Trenger å vite, hvordan man beregner formuekode. Deretter må du finne ut reglene for bruk av en slik kombinasjon.. Blir jeg rik, avhenger ikke bare av koden som oppnås som et resultat av beregningen, men også fra det, hvor riktig det skal brukes.

referanse informasjon

DokumenterRapporterav nevner Dokumentbase SecuritiesAvsetningerFinansielle dokumenterOppløsningerRubrikator etter emne Finans Byer i Den russiske føderasjonenregioner etter eksakte datoerVilkårVitenskapelig terminologi Finansiell økonomiskTidDatoer 2015 2016 Dokumenter i finanssektoren i investeringen

Kombinasjoner uten repetisjoner

En oppgave: Finn alle mulige kombinasjoner uten repetisjoner fra mange elementer {1,2,3} av 2.
Følgende kombinasjoner eksisterer:1: 1 22: 1 33: 2 3
Antall mulige kombinasjoner uten repetisjoner av N-elementer av M kan bestemmes av formelen (N≥M):

det i M! ganger mindre enn tilsvarende antall plasseringer uten repetisjoner (siden kombinasjoner uten repetisjoner ikke avhenger av rekkefølgen til elementene).
Tenk på problemet med å skaffe alle kombinasjoner for tall 1 ... N av M. Implementering i C ++

12345678910111213141516171819202122232425262728293031323334353637383940414243

#inkludere <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int k = m; til (int i = k – 1; Jeg >= 0; –Jeg) hvis (en < n – k + Jeg + 1) { ++en; til (int j = i + 1; j < k; ++j) a = a + 1; return true; } returner falsk;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; til (int i = 0; Jeg < n; i++) cout << en << ” “; cout << endl;}int main() { int n, m, *en; cout << “N = “; cin >> n; cout << “M = “; cin >> m; a = new int; til (int i = 0; Jeg < n; i++) a = i + 1; Print(en, m); hvis (n >= m) { samtidig som (Neste sett(en, n, m)) Print(en, m); } cin.get(); cin.get(); komme tilbake 0;}

Результат выполнения

Engelsk numerologi: konsept og essens

Den eldste kunnskapen, som hjelper til med å forklare, tolke det, hva engler vil fortelle mennesket, kalt engel numerologi.

Minnes, at numerologi studerer vibrasjoner av tall, sifre, deres innflytelse på mennesker og deres livsprosesser. Nok en engelsk matematiker, astrolog John Dee på 1500-tallet skrev et verk om tall, som han betraktet som det universelle englespråket for å kommunisere med mennesker.

Grunnleggeren av den relativt unge undervisningen i Angelic Numerology er Doreen Verche. Klarsynt fra Amerika, psykolog og filosof, forfatter av mange bøker. Hun dedikerte sine arbeider til Supreme Beings, inkludert guder, engler, helgener. I mange år har hun forsket på uforklarlige fenomener.. Men det var verdt det. Hun skapte instrumentet, som kan hjelpe deg med å tolke budskapene til dine hjelpere fra himmelen. I følge Doreen Verce, vi mottar jevnlig tegn fra engler, som advarer om farer, foreslå løsninger på problemer i en persons liv.

Engler snakker med mann etter tall, bokstaver, tegn. Doreen Verces verk snakker om ledetråder fra usynlige keepere, som er kodet i gjentatte sifre eller kombinasjoner derav. Nemlig:

• på bilskilt;
• på klokka;
• i kaken, leilighet, kontor nummerering;
• i fødselsdatoer;
• i billettformer, som i transport, og offentlige fasiliteter, etc..

I alle slike kombinasjoner, tall skjuler data, som kan gjøre justeringer i fremtiden for mennesker. Doreen Verce har forsket mye på temaet, dedikert til numerologiske beregninger etter fødselsdato. Slike beregninger hjelper til med å identifisere barn., som har unike evner fra fødselen, og ikke bare.

Antall treff, kombinasjoner vi ofte ikke legger merke til

Men det er verdt å være oppmerksom på, fordi et slikt fenomen kan være en viktig advarsel. Tross alt sender ikke engler oss et slikt tegn for ingenting

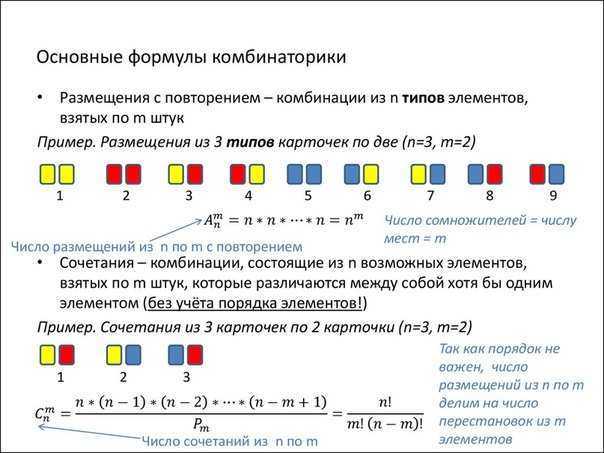
Kombinasjoner med repetisjoner

Kombinasjoner med repetisjoner er sett med M-elementer, der hvert element i settet N kan delta flere ganger. I dette tilfellet pålegges ingen begrensninger på forholdet mellom verdiene M og N, og det totale antall kombinasjoner med repetisjoner er

Et eksempel på et slikt problem er valget av M-postkort fra N på alle mulige måter.

For å generere kombinasjoner med repetisjoner, vil vi bruke løsningen for å generere plassering med repetisjoner., C ++ implementering

1234567891011121314151617181920212223242526272829303132333435363738394041

#inkludere <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int j = m – 1; samtidig som (a == n && j >= 0) j–; hvis (j < 0) returner falsk; hvis (en >= n) j–; a++; hvis (j == m – 1) return true; til (int k = j + 1; k < m; k++) a = a; return true;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; til (int i = 0; Jeg < n; i++) cout << en << ” “; cout << endl;}int main() { int n, m, *en; cout << “N = “; cin >> n; cout << “M = “; cin >> m; int h = n > m ? n : m; // размер массива а выбирается как max(n,m) a = new int; til (int i = 0; Jeg < h; i++) a = 1; Print(en, m); samtidig som (Neste sett(en, n, m)) Print(en, m); cin.get(); cin.get(); komme tilbake 0;}

Resultatet av algoritmen ovenfor:

Algoritmisering

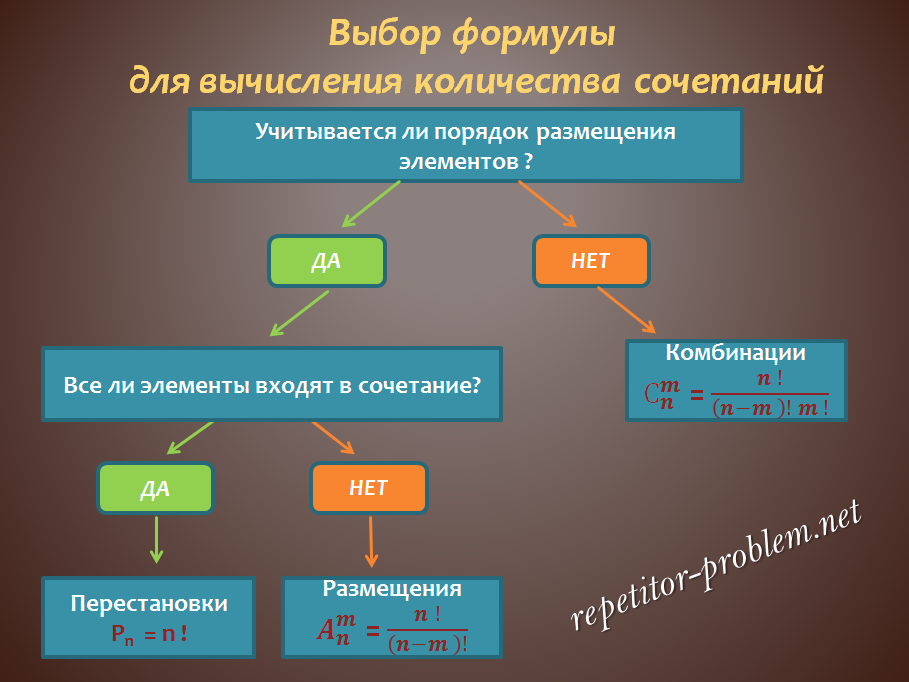
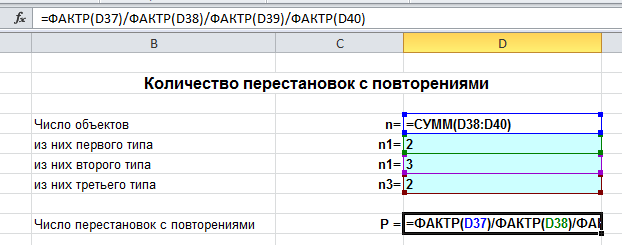
Grunnleggende formel for kombinatorikk

La det være k grupper av elementer, og i-gruppen består av n_Jeg elementer.
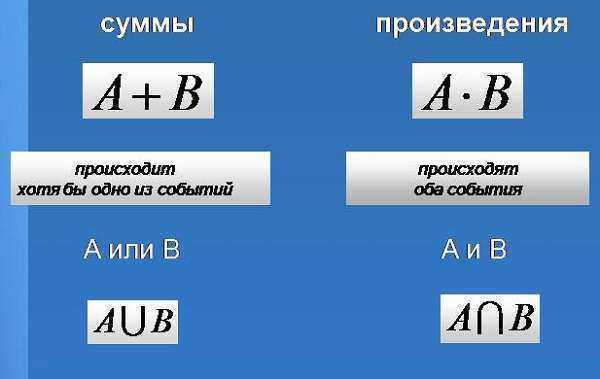
Velg ett element fra hver gruppe. Deretter totalt antall måter,
som et slikt valg kan tas med, er definert av forholdet N = n₁*n₂*n₃*…*n_k.

Eksempel 1. La oss forklare denne regelen på en enkel måte
eksempel. La det være to grupper av elementer, og den første gruppen består av
n₁ elementer, og det andre – av n₂ elementer. hvor mange
forskjellige par av elementer kan være sammensatt av disse to gruppene, på denne måten,
slik at det er ett element i et par fra hver gruppe? La oss innrømme, Vi tok
det første elementet fra den første gruppen og, uten å endre det, gikk over alt mulig
par, bare endre elementer fra den andre gruppen. Slike par for dette elementet
kan være n₂. Så tar vi det andre elementet fra den første gruppen
og komponer også alle mulige par for det. Det vil også være n slike par₂.
Siden den første gruppen bare inneholder n₁ element, alt mulig
alternativene vil være n₁*n₂.Eksempel 2. hvor mange
tresifrede partall kan bestå av sifre 0, 1, 2, 3, 4, 5, 6, hvis
tall kan gjentas?Beslutning: n₁= 6
(fordi. som det første sifferet, kan du ta et siffer fra 1, 2, 3, 4, 5, 6), n₂= 7
(fordi. som andre siffer, kan du ta hvilket som helst siffer fra 0, 1, 2, 3, 4, 5,
6), n₃= 4 (fordi. som det tredje sifferet, kan du ta et siffer fra 0, 2, 4,
6).

så, N = n₁*n₂*n₃= 6 * 7 * 4 = 168.

I så fall, når alle gruppene har like mange elementer, dvs. n₁= n₂=…n_k= n
det kunne vurderes, at hvert valg er tatt fra samme gruppe, dessuten
elementet etter valget går tilbake til gruppen igjen. Deretter tallet på alle måter
valget er nk. Denne typen utvalg i kombinatorikk kalles utvalg med retur.

Eksempel 3. Hvor mange er alle firesifrede tall
kan bestå av tall 1, 5, 6, 7, 8?Beslutning. For hver rang
et firesifret nummer er det fem muligheter, betyr N = 5 * 5 * 5 * 5 = 54 = 625.

Tenk på settet, bestående av n elementer. den
et sett i kombinatorikk kalles generelt
samlet.

Virksomhet og økonomi

BankerRikdom og velferdKorrupsjon(Forbrytelse)MarkedsføringLedelseInvesteringerSikkerhetLedelseOffentlige aksjeselskaperProsjekterDokumenterSikkerhet – kontrollere verdipapirer – Verdsettelsesobligasjoner Gjeld Valuta Eiendom(Leie)YrkerJobberHandelTjenesterFinansiForsikringBudsjettFinansielle tjenester

Hva skal jeg gjøre med mantrikoden når du har fullført ritualet

Etter, hvordan numeriske verdier ble lest under 77 dager, de skal siktes for 4 elementer for videre arbeid.

For å gjøre dette må du utføre enkle manipulasjoner.:

1. Aktiver koden med jordens energi. En liten potte med jord er egnet for ritualet.. Du trenger også blomsterfrø. Dette skal være nøyaktig frøene, ikke skudd og knoller av planter. Etter å ha utarbeidet de nødvendige attributtene, mantraet skal skrives på et blankt papir og begraves i bakken, og sa ordene tre ganger - “Jorden er full av rikdom, du er nå drømmen min ”. Deretter legges et blomsterfrø i potten.
2. Etter jordelementet er mantraet ladet med vannens energi. Dette ritualet består i å vanne frøet, som er ledsaget av ordene “Vann og jord, gjenopplive frøene ”. Som i forrige tilfelle, gjøre en uttalelse 3 ganger.
3. Deretter kommer turen til elementene i Air. Gryten med det fremtidige anlegget bør bringes til et åpent vindu og sa: "Du, Luft, jeg trenger, som lys, og gi drømmen min Dawn ". Det må gjentas innenfra 3 dager.
4. Når en frøspire dukker opp, det er tid for elementene i ild. Det kreves et nytt tent lys for å vekke mantraet. Den må plasseres ved siden av anlegget og, konsentrere seg, si tre ganger: "Det brenner, Brann, stearinlys - brenn ut, og ødelegge fattigdom. La spiren vokse, hva glir pengene gjemmer seg. Og jeg vil blomstre med ham, tiltrekke rikdom i penger ".

Etter disse trinnene begynner valutakoden å fungere. Det er tilrådelig å ikke kaste potten med spire og mantra, fortsetter vanlig pleie av planten.

I tillegg, for å forbedre effekten av mantrikoden, du kan bruke bildet av tall på et papp med grønt og rødt blekk. En slik pengetalisman må hele tiden bæres med deg..

Magien til kjente ting

Vår tilfeldige tilfeldige tallgenerator online.

Våre randomiseringsgeneratorer krever ikke nedlasting til din personlige PC. Alt skjer i online nummergenerator-modus. Bare spesifiser disse parametrene, som: antall numre online, hvor tall vil bli valgt tilfeldig. Angi også antall tall, som vil bli valgt.
For eksempel, у Вас есть группа Вконтакте. В группе вы разыгрываете 5 premier, blant deltakerne, som vil legge om rekorden. Ved hjelp av en dedikert app, vi fikk en liste over deltakere. Hver har blitt tildelt et løpenummer for numre online.

Gå nå til vår online generator og spesifiser antall numre (antall deltakere). for eksempel, spørre, hvilke tall på nettet trenger 5, siden vi har 5 premier. Теперь жмем кнопку генерации. Så får vi 5 tilfeldige tall på nettet, som strekker seg fra 1 til 112 inklusive. Generert 5 nummer på nettet vil tilsvare serienummeret på fem deltakere, som ble vinnerne av tegningen. Alt er enkelt og praktisk.

Et annet pluss av tilfeldig tallgenerator er, at alle tall på nettet blir gitt tilfeldig. Det vil si å påvirke ham, eller beregne, hvilket nummer blir neste, virker ikke mulig. Hva generatoren gjør kan sies, ærlig og pålitelig, og administrasjonen, som gir bort premier ved hjelp av vår gratis generator, ærlig og anstendig i møte med deltakerne i konkurransen. Og hvis du er i tvil om en løsning, så kan du bruke vår ja eller nei-svargenerator.

Hvordan beregne formuekoden din

Det er gode og dårlige kombinasjoner

Numerologi og penger er nært beslektet. Det er tallkombinasjoner, velstandsgenererende, men det er mislykkede kombinasjoner. Hvis du bruker dem riktig, suksess og flaks vil være på din side. Det er enkelt å beregne koden. For å gjøre dette må du utføre følgende beregninger:

• skriv nummeret ditt på et blankt papir, måned og fødselsår (f.eks, 31.10.1987);
• for å beregne suksessverdien, de to første sifrene skal legges til, dvs, spesifikk fødselsdato (f.eks, 31 - 3 + 1 = 4). Dette tallet vil være det første i kombinasjonen;
• for å beregne det andre tegnet i kombinasjonen, det er nødvendig å beregne månedens verdi (f.eks, oktober, 10 måned - 1 + 0 = 1);
• nå må du beregne mengden av fødselsåret (f.eks, 1987 - 1 + 9 + 8 + 7 = 25, 2+5= 7);
• til slutt må du personlig beregne det siste tegnet i kombinasjonen, for dette er alle tre tidligere mottatte tall oppsummert (f.eks, 4+1+7= 12, 1+2= 3, i dette tilfellet er pengene kombinasjonen 4173). Den resulterende kombinasjonen er en personlig kode for en person..

I tillegg til den personlige koden, det er universelle verdier, at alle kan søke, som en millionær, og med mellominntekt. Dette er en digital maskot, som er avbildet i form av fire åtterer av samme størrelse. Denne kombinasjonen er veldig sterk, betyr pengesuksess og stabilitet.

Du kan også beregne da, vil jeg være rik, ved navn. For dette er det tatt en oversiktstabell mellom bokstaver og tall. For eksempel, Marina, som ble født 5 tall. I dette tilfellet er det bare bursdagen som er tatt:

M-5, A-1, R-9, I-1, N-6, A-1. 5+1+9+1+6+1= 23, 2+3= 5. Deretter legger du til fødselsdatoen - 5 + 5 = 10, 1+0= 1 - en og er koden for lykke og penger for en bestemt person. Men kan han lykkes, kommer an på, hvor godt det brukes.

Permutasjoner av n elementer

Definisjon 3. Permutasjon
av n elementer
ethvert bestilt sett kalles
disse elementene.

Eksempel 7a. Alle slags permutasjoner
mengder, bestående av tre elementer {1, 2, 3} er: (1, 2, 3), (1, 3,
2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

Antall tydelige permutasjoner av n elementer er betegnet med P_n og
beregnes med formelen P_n= n!.

Eksempel 8. På hvor mange måter syv bøker
forskjellige forfattere kan ordnes i en rad på hyllen?Beslutning:dette problemet om nummeret
omorganisering av syv forskjellige bøker. Det er P₇= 7!= 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040
måter å ordne bøker på.

Diskusjon. Vi ser,
at antall mulige kombinasjoner kan beregnes etter forskjellige regler
(kombinasjonsmuligheter, kombinasjoner, plassering) og resultatet blir annerledes,
fordi. prinsippet om telling og selve formlene er forskjellige. Ser nøye på
definisjoner, kan bli sett, at resultatet avhenger av flere faktorer
samtidig.
Først, fra det, fra hvor mange elementer kan vi kombinere dem
settene (hvor stor er den totale populasjonen av elementer).
for det andre, resultatet avhenger av, hvor store er settene med elementer for oss
trenge

Og det siste, det er viktig å vite, er for oss
viktig rekkefølge på varene i et sett. La oss forklare den siste faktoren på
følgende eksempel

Eksempel 9. På foreldremøtet
tilstede 20 Mann. Hvor mange forskjellige komposisjonsalternativer er det
foreldreutvalg, hvis det skulle komme inn 5 Mann?Beslutning: I dette eksemplet, vi
ikke interessert i rekkefølgen på navnene i utvalgslisten. Hvis, som et resultat, i hans
komposisjonen vil være de samme menneskene, da er betydningen for oss den samme
alternativ. Derfor kan vi bruke formelen til å beregne antall kombinasjoner fra 20 elementer av 5.
Ting vil være annerledes, hvis hvert komitemedlem opprinnelig er ansvarlig for
bestemt arbeidsretning. Da med samme lønn
komiteen, inne er det mulig 5! permutasjonsalternativer, hvilken betydning. Antall
forskjellig (og komposisjon, og etter ansvarsområde) alternativene definert i
i dette tilfellet antall plasseringer
av 20 elementer av 5.

Selvtestoppgaver
1. Hvor mange tresifrede partall som kan lages fra sifre 0, 1, 2, 3, 4, 5,
6, hvis tall kan gjentas?
Siden. et partall på tredjeplass kan være 0, 2, 4, 6, dvs. firesifret. Hvilke som helst av de syv sifrene kan være på andreplass. Enhver av syv andre sifre enn null kan være i utgangspunktet, dvs. 6 muligheter. Resultat = 4 * 7 * 6 = 168.
2. Hvor mange femsifrede tall er der, som leser det samme til venstre
høyre og høyre mot venstre?
Ethvert tall kan være i utgangspunktet bortsett fra 0, dvs. 9 muligheter. Et hvilket som helst tall kan være på andreplass, dvs. 10 muligheter. Ethvert nummer fra, dvs. 10 muligheter. Det fjerde og femte tallet er forhåndsdefinert, de matcher første og andre, derav, antall slike tall er 9 * 10 * 10 = 900.
3. Det er ti emner og fem leksjoner per dag i klassen. På mange måter kan du
lage en tidsplan for en dag?
4. Hvor mange måter du kan velge 4 delegere til konferansen, hvis du er i en gruppe
20 Mann?

n = C₂₀4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)= 4845.

5. Hvor mange måter kan åtte forskjellige bokstaver spaltes i åtte
forskjellige konvolutter, hvis bare en bokstav legges i hver konvolutt?
Du kan legge i den første konvolutten 1 på åtte bokstaver, i den andre av de syv gjenværende, i den tredje av seks osv.. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Tre matematikere og ti økonomer må være sammensatt av en kommisjon,
bestående av to matematikere og seks økonomer. Hvor mange måter er det
kan bli gjort?

Antall måter å velge matematikk C₃2= 3!/(2!*(3-2))!= 3/2, antall måter å velge økonom C₁₀6= 10!/(6!*(10-6))!= 7 * 8 * 9 * 10 /(1*2*3*4)= 210. n = C₃2*FRA₁₀6= 3 * 210 = 630.