Qual a melhor loteria

A regra 4. Comece na hora

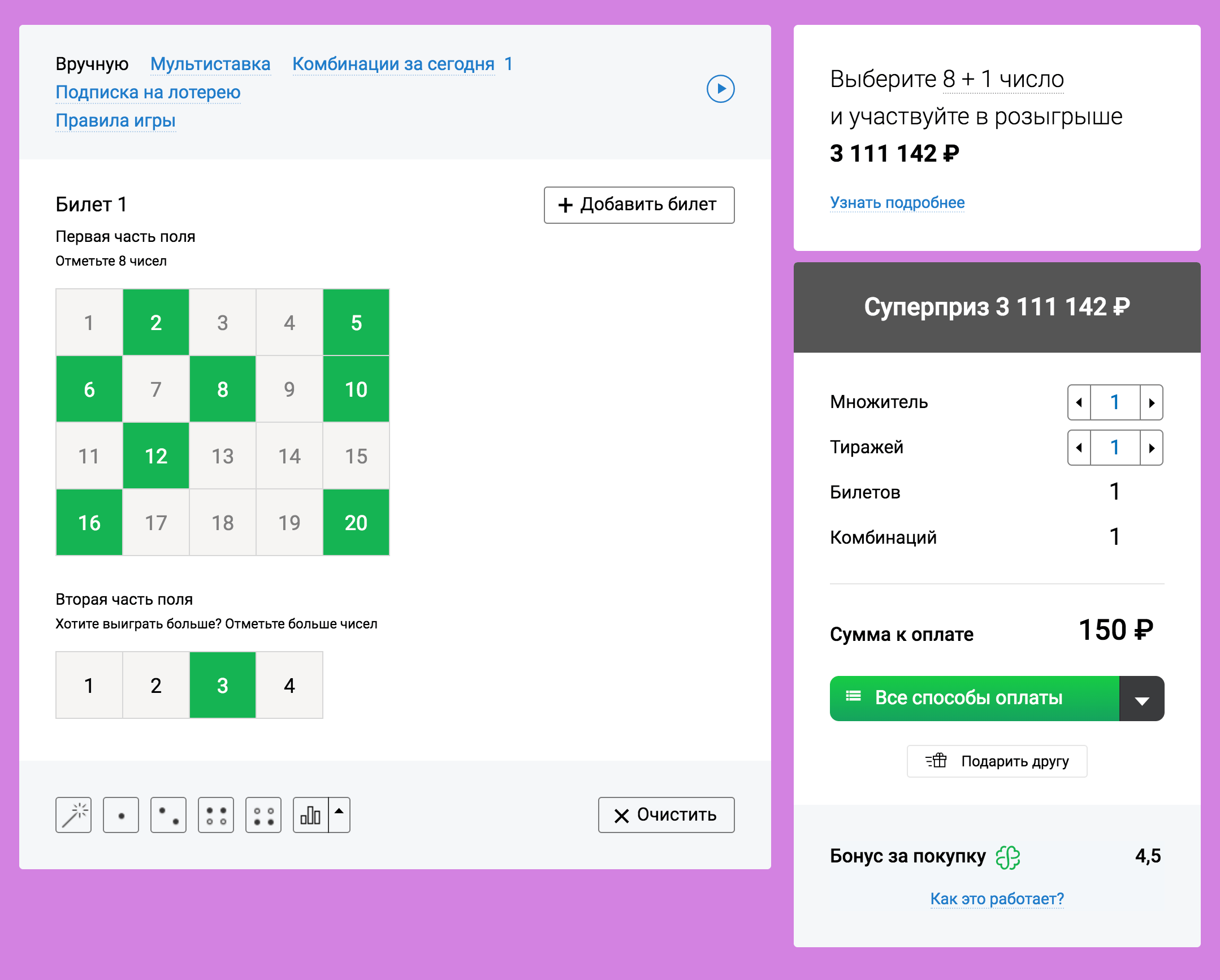
Bilhete de loteria PowerBall, a propósito, que vale a pena 2 dólar. Para calcular os benefícios, que pagaria a compra de um bilhete, нужно умножить цену билета на 292 201 338.

Mais sobre cálculos. Esta é uma referência ao primeiro ponto., onde diz, que o benefício de uma solução é igual ao seu valor, multiplicado pela probabilidade. Se tivermos um evento com probabilidade 1 / X e valor N, então o benefício será N / X. Мы тратим 2 доллара и можем подсчитать, quanto a vitória pagaria pela compra do ingresso:

• 2 = N ÷ X.
• N = 2 × X, а X тут как раз равен 292 201 338, como mostrado pelos cálculos da parte anterior.

Você também precisa levar em consideração os impostos (descobrir, que porcentagem do valor declarado irá realmente para o vencedor, normalmente é sobre 70%). То есть джекпот должен составлять как минимум 850 Milhão de dolares, e isso acontece nesta loteria. Como assim, Eu disse no começo, que o ganho em tal multiplicação nem sempre é a favor do jogador?

O fato, e se o jackpot não tiver sido sorteado, então vai da próxima vez, e é por isso que o dinheiro se acumula por um tempo, e as vendas de ingressos continuam.

Mas é impossível saber com antecedência. No entanto, você pode começar a comprar ingressos, assim que o tamanho do jackpot exceder o valor mencionado. Em tal situação, matematicamente, o jogo será benéfico.

Você ainda pode entender, o que é mais lucrativo: compre muitos bilhetes para um jogo ou compre um bilhete para muitos jogos? Vamos pensar.

Na teoria da probabilidade, há um conceito de eventos não relacionados. Isso significa, que o resultado de um evento não afeta o resultado de outro. por exemplo, se você lançar dois dados, então os números decrescentes sobre eles não estão relacionados: em termos de aleatoriedade, um dado não afeta o comportamento do outro. Mas se você tirar duas cartas do baralho, então esses eventos estão conectados, porque o primeiro cartão depende de, quais cartas permanecerão no baralho.

Um equívoco popular sobre isso é chamado de erro do jogador.. Surge da ideia intuitiva de uma pessoa da conexão de eventos não relacionados.

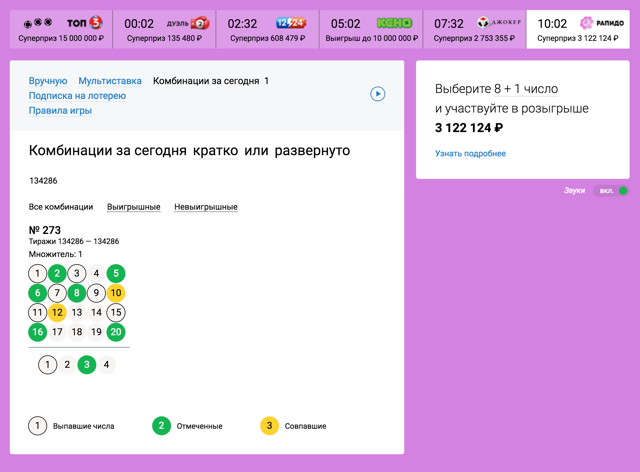
Voltando às loterias: jogos diferentes são eventos não relacionados, porque a sequência de bolas é re-selecionada. Portanto, as chances de ganhar qualquer loteria em particular não dependem de, quantas vezes você já jogou antes. É muito difícil aceitar intuitivamente., porque uma pessoa toda vez, comprando um ingresso, acha: “Bem, agora você tem sorte, quanto tempo para, Eu tenho jogado muito tempo!" Mas não, a teoria da probabilidade é uma coisa sem coração.

Mas comprar vários ingressos para um jogo aumenta suas chances proporcionalmente, porque os ingressos dentro de um jogo estão empatados: se um ganha, significa, de outros (com outra combinação) definitivamente não vai ganhar. Покупка 10 билетов увеличивает шансы в 10 Tempo, se todas as combinações nos ingressos forem diferentes (na verdade, quase sempre é). Em outras palavras, если у вас есть деньги на 10 ingressos, é melhor comprá-los para um jogo, чем покупать по билету на 10 jogos.

Se você tirar um tíquete do seu salário uma vez por mês, por causa de, então, provável, o processo de jogar é importante para você. Математически выгоднее скопить эти деньги и в конце года купить сразу 12 ingressos, Apesar, claro, perder em tal situação será percebido de forma mais devastadora.

A regra 1. Avalie os riscos

Não é segredo para uma pessoa iluminada moderna, que os cassinos e vários estabelecimentos de jogos de azar calculem todos os seus jogos como, ser sempre o vencedor e ter lucro. Isso é feito de forma muito simples: a pessoa precisa devolver os ganhos, que se correlaciona com a sua aposta baixa em comparação com as suas chances de ganhar.

Não há exceções, a menos que alguém especificamente queira lhe dar dinheiro. Mantenha esta regra simples em mente, sempre olhar para a situação sobriamente.

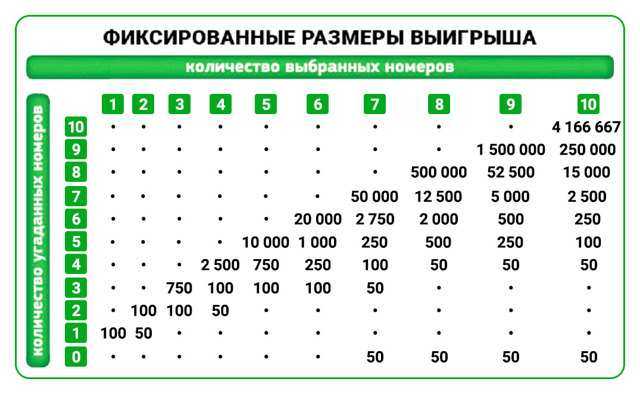
A teoria dos jogos avalia qualquer estratégia da mesma maneira: a probabilidade de obter uma vitória é multiplicada por seu tamanho. A grosso modo, matemática conta, что гарантированно получить 1 000 рублей — это как получить 2 000 рублей с 50-процентным шансом. Este princípio dá a você a capacidade de comparar jogos diferentes uns com os outros.. O que é melhor: миллион долларов с шансом 1/100 000 ou 50 долларов с шансом 1/4? Parece intuitivo, que a primeira frase é mais interessante, mas o último é matematicamente mais vantajoso.

Se você ficar dentro da estrutura da matemática sozinho, pode ser calculado: é impossível ganhar no casino, porque qualquer estratégia escolhida leva a, que o produto da probabilidade de ganhar pelo tamanho do pagamento para o jogador é sempre menor que a aposta, o que ele já fez.

E também porque, esse dinheiro não é linear para nós: формально получить 1 рубль прямо сейчас — это как получить миллион рублей с шансом 1/1 000 000, mas, na verdade, a perda do rublo não afetará nossa condição de forma alguma, nada vai mudar na vida, mas ganhar um milhão é um evento muito sério.