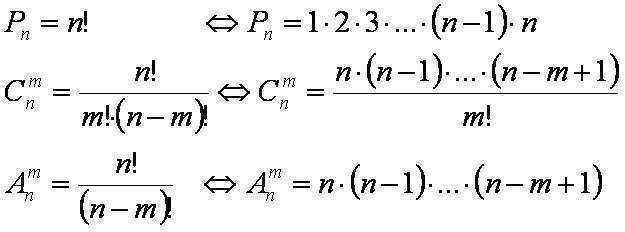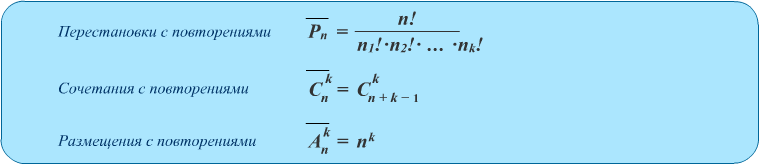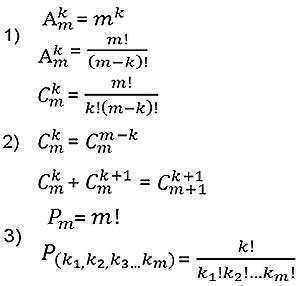Kombinatoriska element

Pengarnas magi i numerologi

Varje nummer har sin egen energi och påverkar människans liv på ett visst sätt.. Numerologi av pengar hjälper till att bestämma betydelsen av ett nummer, ta reda på den personliga koden för pengar och rikedom. Fiskekoden beräknas med hjälp av födelsedatum. Då måste du se transkriptet. Du måste också veta, hur du använder din förmögenhetskod korrekt.

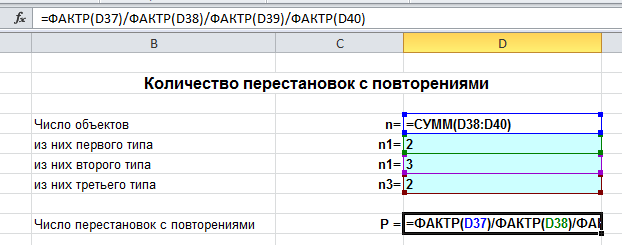
Det viktigaste är att korrekt beräkna den finansiella koden

Förutom, vad är antalet förmögenhet?, det finns också siffror, inte ger överflöd i en människas liv. De måste undvikas. Att locka ekonomiskt flöde, måste bekanta dig med, vad står varje nummer för:

1. Noll och en. Numerologer tror, att dessa siffror och koder är negativa för monetär energi, de ger inte lycka till. Därför bör du undvika besparingar., insättningar med belopp, där dessa siffror finns, eftersom de kommer att sakta ner kassaflödet och inte kommer att ge välstånd och framgång.
2. Två. Det här är en olycklig siffra. Hon kommer inte att ge välstånd och framgång. Det rekommenderas inte att använda sedlar av denna valör för besparingar, bär inte dem i din plånbok.
3. Trekant. Är ekonomiskt gynnsam, med sin hjälp kan en person vinna lotteriet, hitta ytterligare inkomstkällor. Men numerologer rekommenderar inte att man samlar in medel., vars summa är 300, 3000, 30000. Denna siffra behöver ständig rörelse, hon behöver energi, inte fred. Det bästa är att köpa en lotteri för ett sådant belopp eller investera i ditt eget företag..
4. De fyra i den personliga koden är en symbol för stabilitet, pålitlighet. Perfekt för besparingar, besparingar, investering är mängden räkningar 400, 4000, 40000. På det här sättet, välstånd kommer att öka.
5. Fem är en mycket viktig numerisk förmögenhetskod inom numerologi. Räkningar med detta nummer är magneter med riktiga pengar.. De kan lånas ut, spendera på resor, ackumulera, spendera så, som du vill.
6. En sådan finansiell kod kan innebära vissa ekonomiska begränsningar.. Med denna siffra lär folk sig att spara, kontrollera dina utgifter. Belopp 600, 6000 är en symbol för stabilitet och säkerhet. Numerologer rekommenderar inte att man investerar sådana belopp.
7. Sju är kod, otur, den kan inte användas för lagring, investeringar, besparingar, lån och andra finansiella transaktioner, som är förknippade med risk.
8. Åtta är en stark välfärdskod inom numerologi, han anses vara mycket framgångsrik. Insättningar för belopp 800, 8000, 80000 är mycket framgångsrika, de lockar pengar, som en magnet.
9. Nio är en symbol för andlighet och inre utveckling. Att samla in pengar med det kommer inte att hända, men det blir ingen förlust heller. Det rekommenderas att spendera summor med en nio på självstudier, Träning

Att använda siffror korrekt, behöver veta, hur man beräknar förmögenhetskod. Därefter måste du ta reda på reglerna för att använda en sådan kombination.. Blir jag rik, beror inte bara på koden som erhållits till följd av beräkningen, men också från det, hur korrekt att använda den.

referensinformation

DokumentRapporterav nämner Dokumentbas SäkerheterAvsättningarFinansiella dokumentUpplösningarRubrik efter ämne Finans Ryska federationens städer vid exakta datumVillkorVetenskaplig terminologi Ekonomisk ekonomiTidDatum 2015 2016 Dokument i den finansiella sektorn i investeringen

Kombinationer utan upprepningar

En uppgift: Hitta alla möjliga kombinationer utan upprepningar från många element {1,2,3} förbi 2.
Följande kombinationer finns:1: 1 22: 1 33: 2 3
Antalet möjliga kombinationer utan upprepningar av N-element av M kan bestämmas med formeln (N≥M):

det i M! gånger mindre än motsvarande antal placeringar utan repetitioner (eftersom kombinationer utan upprepningar inte beror på elementens ordning).
Tänk på problemet med att få alla kombinationer för siffrorna 1 ... N av M. Implementering i C ++

12345678910111213141516171819202122232425262728293031323334353637383940414243

#omfatta <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int k = m; för (int i = k – 1; i >= 0; –i) om (a < n – k + i + 1) { ++a; för (int j = i + 1; j < k; ++j) a = a + 1; return true; } returnera falsk;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; för (int i = 0; i < n; i++) cout << a << ” “; cout << endl;}int main() { int n, m, *a; cout << “N = “; cin >> n; cout << “M = “; cin >> m; a = new int; för (int i = 0; i < n; i++) a = i + 1; Print(a, m); om (n >= m) { medan (Nästa uppsättning(a, n, m)) Print(a, m); } cin.get(); cin.get(); lämna tillbaka 0;}

Результат выполнения

Engelsk numerologi: koncept och essens

Den äldsta kunskapen, som hjälper till att förklara, tolka det, vad änglar vill berätta för människan, kallad änglisk numerologi.

Återkallelse, att numerologi studerar vibrationerna i tal, siffror, deras inflytande på människor och deras livsprocesser. En annan engelsk matematiker, astrologen John Dee på 1500-talet skrev ett arbete om siffror, som han betraktade som det universella ängelspråket för att kommunicera med människor.

Grundaren av den relativt unga undervisningen i Angelic Numerology är Doreen Verche. Klarsynta från Amerika, psykolog och filosof, författare till många böcker. Hon ägnade sina verk till Supreme Beings, inklusive gudar, änglar, helgon. I många år har hon forskat om oförklarliga fenomen.. Men det var värt det. Hon skapade instrumentet, som kan hjälpa dig att tolka budskapen från dina hjälpare från himlen. Enligt Doreen Verce, vi får regelbundet tecken från änglar, som varnar för faror, föreslå lösningar på problem i en människas liv.

Änglar pratar med människan i siffror, brev, tecken. Doreen Verces verk talar om ledtrådar från osynliga djurhållare, som är kodade i upprepade siffror eller kombinationer därav. Nämligen:

• på bilskyltar;
• på klockan;
• i kakan, lägenhet, kontorsnummerering;
• i födelsedatum;
• i biljettformulär, som i transport, och offentliga anläggningar etc..

I alla sådana kombinationer, siffror döljer data, som kan göra anpassningar till människors framtid. Doreen Verce har forskat mycket i ämnet, tillägnad numerologiska beräkningar efter födelsedatum. Sådana beräkningar hjälper till att identifiera barn., som har unika förmågor från födseln, och inte bara.

Antal matchningar, kombinationer som vi ofta inte märker

Men det är värt att vara uppmärksam på, eftersom ett sådant fenomen kan vara en viktig varning. När allt kommer omkring änglar skickar inte oss ett sådant tecken för ingenting

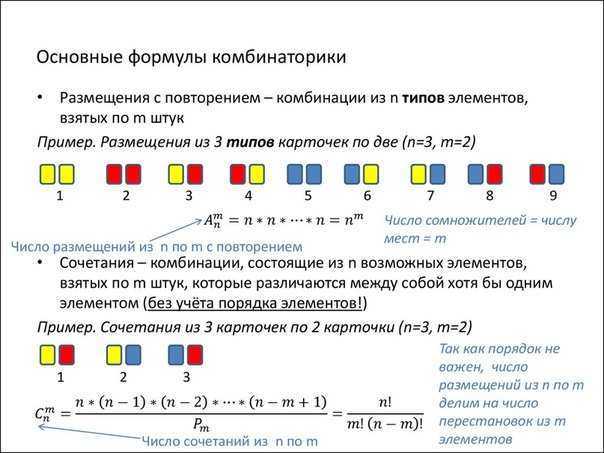
Kombinationer med upprepningar

Kombinationer med upprepningar är uppsättningar av M-element, där varje element i uppsättningen N kan delta flera gånger. I detta fall införs inga begränsningar för förhållandet mellan värdena M och N, och det totala antalet kombinationer med repetitioner är

Ett exempel på ett sådant problem är valet av M-vykort från N på alla möjliga sätt.

För att generera kombinationer med repetitioner använder vi lösningen för att generera placeringar med repetitioner., C ++ - implementering

1234567891011121314151617181920212223242526272829303132333435363738394041

#omfatta <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int j = m – 1; medan (a == n && j >= 0) j–; om (j < 0) returnera falsk; om (a >= n) j–; a++; om (j == m – 1) return true; för (int k = j + 1; k < m; k++) a = a; return true;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; för (int i = 0; i < n; i++) cout << a << ” “; cout << endl;}int main() { int n, m, *a; cout << “N = “; cin >> n; cout << “M = “; cin >> m; int h = n > m ? n : m; // размер массива а выбирается как max(n,m) a = new int; för (int i = 0; i < h; i++) a = 1; Print(a, m); medan (Nästa uppsättning(a, n, m)) Print(a, m); cin.get(); cin.get(); lämna tillbaka 0;}

Resultatet av ovanstående algoritm:

Algoritmisering

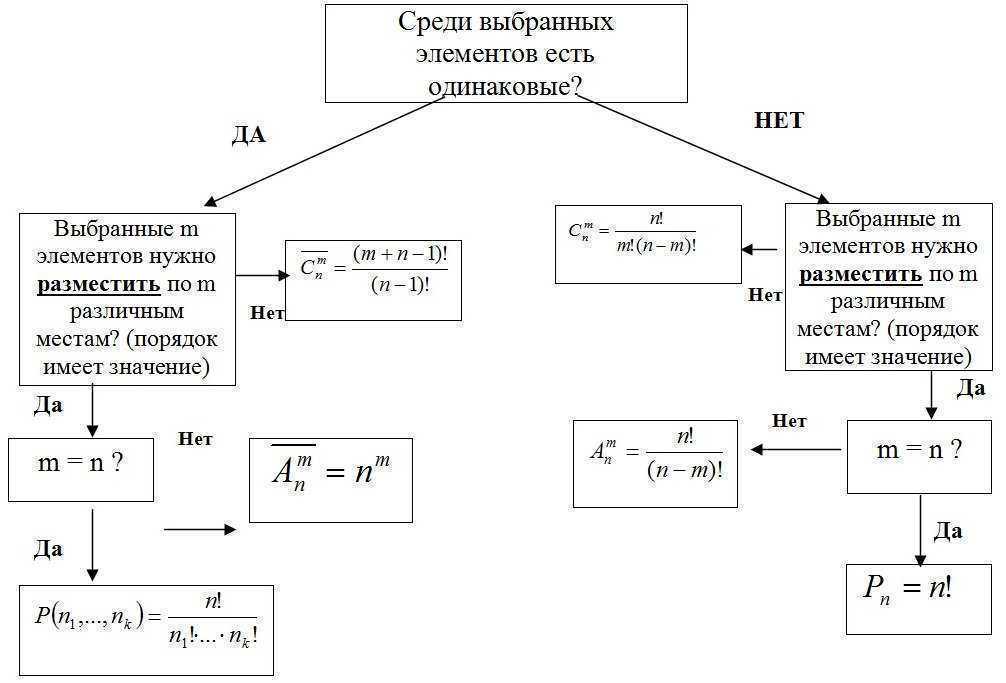
Grundformel för kombinatorik

Låt det finnas k grupper av element, och den i-gruppen består av n_i element.
Välj ett element från varje grupp. Sedan totalt antal vägar,
med vilket ett sådant val kan göras, definieras av relationen N = n₁*n₂*n₃*…*n_k.

Exempel 1. Låt oss förklara denna regel på ett enkelt sätt
exempel. Låt det finnas två grupper av element, och den första gruppen består av
n₁ element, och den andra – av n₂ element. hur många
olika par av element kan bestå av dessa två grupper, på det här sättet,
så att det finns ett element i ett par från varje grupp? Låt oss erkänna, Vi tog
det första elementet från den första gruppen och, utan att ändra det, gick över allt möjligt
par, ändra bara element från den andra gruppen. Sådana par för detta element
kan vara n₂. Sedan tar vi det andra föremålet från den första gruppen
och komponera också alla möjliga par för det. Det kommer också att finnas n sådana par₂.
Eftersom den första gruppen endast innehåller n₁ element, allt möjligt
alternativen kommer att vara n₁*n₂.Exempel 2. hur många
tresiffriga jämna siffror kan bestå av siffror 0, 1, 2, 3, 4, 5, 6, om
siffror kan upprepas?Beslut: n₁= 6
(eftersom. som första siffra kan du ta vilken siffra som helst från 1, 2, 3, 4, 5, 6), n₂= 7
(eftersom. som andra siffra kan du ta vilken siffra som helst från 0, 1, 2, 3, 4, 5,
6), n₃= 4 (eftersom. som tredje siffra kan du ta vilken siffra som helst från 0, 2, 4,
6).

så, N = n₁*n₂*n₃= 6 * 7 * 4 = 168.

Isåfall, när alla grupper har samma antal element, dvs.. n₁= n₂=…n_k= n
det kan övervägas, att varje val görs från samma grupp, dessutom
elementet efter valet återgår till gruppen igen. Sedan antalet alla vägar
valet är nk. Denna typ av urval i kombinatorik kallas urval med retur.

Exempel 3. Hur många är alla fyrsiffriga siffror
kan bestå av siffror 1, 5, 6, 7, 8?Beslut. För varje rang
ett fyrsiffrigt nummer finns fem möjligheter, betyder N = 5 * 5 * 5 * 5 = 54 = 625.

Tänk på uppsättningen, bestående av n element. Det
en uppsättning i kombinatorik kallas allmän
aggregat.

Företag och ekonomi

BankerVälstånd och välfärdKorruption(Brottslighet)MarknadsföringFörvaltningInvesteringarSäkerhetFörvaltningOffentliga aktiebolagProjektDokumentSäkerhet – kontrollera värdepapper – Värderingsobligationer Skulder Valuta Fastigheter(Hyra)Yrken Jobb Handlar Tjänster Finansiering Försäkring Budget Budget Finansiella tjänster

Vad man ska göra med mantric-koden efter att ha fullbordat ritualen

Efter, hur numeriska värden lästes under 77 dagar, de borde debiteras för 4 element för vidare arbete.

För att göra detta måste du utföra enkla manipuleringar.:

1. Aktivera koden med jordens energi. En liten jordkruka är lämplig för ritualen.. Du behöver också blommor. Dessa borde vara exakt frön., inte skott och knölar från växter. Efter att ha förberett de nödvändiga attributen, mantrat bör skrivas på ett tomt papper och begravas i marken, säger orden tre gånger - ”Jorden är full av rikedomar, du är nu min dröm ”. Därefter placeras ett blommafrö i potten.
2. Efter jordelementet laddas mantrat med vattenens energi. Denna ritual består av att vattna utsäde, som åtföljs av orden ”Vatten och jord, återuppliva fröna ”. Som i föregående fall, gör ett uttalande 3 gånger.
3. Därefter kommer turen till elementen i Air. Krukan med den framtida växten bör föras till ett öppet fönster och sa: "Du, Luft, jag behöver, som ljus, och ge min dröm Dawn ". Det måste upprepas inom 3 dagar.
4. När en fröspira dyker upp, det är dags för eldens element. Ett nytt tänt ljus krävs för att väcka mantrat. Den måste placeras bredvid anläggningen och, koncentrera sig, säg tre gånger: "Det brinner, Brand, ljus - bränn ut, och förstöra fattigdom. Låt groden växa, vad glider pengarna undan?. Och jag kommer att blomstra med honom, locka rikedom i pengar ".

Efter dessa steg börjar valutakoden fungera. Det är tillrådligt att inte kasta bort potten med groden och mantrat, fortsätter den vanliga vården av växten.

Förutom, för att förbättra effekten av mantric-koden, du kan använda bilden av siffror på ett pappark med grönt och rött bläck. En sådan pengar talisman måste ständigt bäras med dig..

Magin med bekanta saker

Vår slumpmässiga slumptalsgenerator online.

Vår randomiseringsgenerator behöver inte laddas ner till din personliga dator. Allt händer i online-nummergeneratorläget. Ange bara dessa parametrar, som: antal nummer online, där siffror kommer att väljas slumpmässigt. Ange också antalet nummer, som kommer att väljas.
Till exempel, у Вас есть группа Вконтакте. В группе вы разыгрываете 5 priser, bland deltagarna, som kommer att lägga om posten. Med hjälp av en dedikerad app, vi har en lista med deltagare. Var och en har tilldelats ett löpnummer för nummer online.

Gå nu till vår onlinegenerator och ange nummerserien (antal deltagare). till exempel, fråga, vilka siffror online behöver 5, eftersom vi har 5 priser. Теперь жмем кнопку генерации. Sedan får vi 5 slumpmässiga nummer online, som sträcker sig från 1 till 112 inklusive. Genererad 5 nummer online kommer att motsvara serienumret på fem deltagare, som blev vinnarna av ritningen. Allt är enkelt och bekvämt.

Ett annat plus av slumptalsgeneratorn är, att alla nummer online ges slumpmässigt. Det vill säga att påverka honom, eller beräkna, vilket antal kommer nästa, verkar inte möjligt. Vad generatorn gör kan sägas, Ärlig och pålitlig, och administrationen, som ger bort priser med vår gratisgenerator, ärlig och anständig inför deltagarna i tävlingen. Och om du är i tvivel om en lösning, då kan du använda vår ja eller nej svar generator.

Hur man beräknar din förmögenhetskod

Det finns bra och dåliga kombinationer

Numerologi och pengar är nära besläktade. Det finns nummerkombinationer, generera välstånd, men det finns misslyckade kombinationer. Om du använder dem korrekt, framgång och tur kommer att vara på din sida. Det är enkelt att beräkna koden. För att göra detta måste du utföra följande beräkningar:

• skriv ditt nummer på ett tomt papper, månad och födelseår (t.ex, 31.10.1987);
• för att beräkna framgångsvärdet, de två första siffrorna ska läggas till, dvs, specifikt födelsedatum (t.ex, 31 - 3 + 1 = 4). Detta nummer blir det första i kombinationen;
• för att beräkna kombinationens andra tecken, det är nödvändigt att beräkna månadens värde (t.ex, Oktober, 10 månad - 1 + 0 = 1);
• nu måste du beräkna beloppet för födelseåret (t.ex, 1987 - 1 + 9 + 8 + 7 = 25, 2+5= 7);
• i slutet måste du personligen beräkna kombinationens sista karaktär, för detta sammanfattas alla tre tidigare mottagna siffrorna (t.ex, 4+1+7= 12, 1+2= 3, i det här fallet är pengarkombinationen 4173). Den resulterande kombinationen är en personlig kod för en person..

Förutom den personliga koden, det finns universella värden, att alla kan ansöka, som en miljonär, och med medelinkomst. Detta är en digital maskot, som avbildas i form av fyra åttor av samma storlek. Denna kombination är mycket stark, betyder monetär framgång och stabilitet.

Du kan också beräkna då, ska jag vara rik, vid namn. För detta tas en överensstämmelsetabell mellan bokstäver och siffror. Till exempel, Marina, som föddes 5 tal. I det här fallet tas bara födelsedagen:

M-5, A-1, R-9, I-1, N-6, A-1. 5+1+9+1+6+1= 23, 2+3= 5. Lägg sedan till födelsedatum - 5 + 5 = 10, 1+0= 1 - en och är koden för lycka och pengar för en viss person. Men kan han lyckas, beror på, hur bra den används.

Permutationer av n element

Definition 3. Permutation
av n element
någon beställd uppsättning kallas
dessa element.

Exempel 7a. Alla typer av permutationer
folkmassor, bestående av tre element {1, 2, 3} är: (1, 2, 3), (1, 3,
2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

Antalet distinkta permutationer av n element betecknas med P_n och
beräknas med formeln P_n= n!.

Exempel 8. På hur många sätt sju böcker
olika författare kan ordnas i en rad på hyllan?Beslut:detta problem om numret
omorganisera sju olika böcker. Det finns P₇= 7!= 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040
sätt att ordna böcker.

Diskussion. Vi ser,
att antalet möjliga kombinationer kan beräknas enligt olika regler
(permutationer, kombinationer, placering) och resultatet blir annorlunda,
eftersom. räkningsprincipen och själva formlerna är olika. Tittar noga på
definitioner, kan ses, att resultatet beror på flera faktorer
på samma gång.
I början, från det, från hur många element vi kan kombinera dem
uppsättningar (hur stor är den totala populationen av element).
För det andra, resultatet beror på, hur stora är uppsättningarna av element för oss
behöver

Och den sista, det är viktigt att veta, är för oss
viktig ordning på artiklar i en uppsättning. Låt oss förklara den sista faktorn
följande exempel

Exempel 9. På föräldermötet
närvarande 20 man. Hur många olika kompositionsalternativ finns det
föräldrakommitté, om det skulle komma in 5 man?Beslut: I detta exempel, vi
inte intresserad av namnordningen i kommittélistan. Om, som ett resultat, i hans
kompositionen kommer att vara samma människor, då är meningen för oss densamma
alternativ. Därför kan vi använda formeln för att beräkna antalet kombinationer från 20 element av 5.
Saker kommer att vara annorlunda, om varje kommittémedlem ursprungligen är ansvarig för
bestämd arbetsriktning. Sedan med samma lön
utskott, inuti är det möjligt 5! permutationsalternativ, vilken roll. siffra
annorlunda (och komposition, och efter ansvarsområde) alternativ definierade i
i det här fallet antalet placeringar
av 20 element av 5.

Självtestuppgifter
1. Hur många tresiffriga jämna nummer kan göras från siffror 0, 1, 2, 3, 4, 5,
6, om siffror kan upprepas?
Eftersom. ett jämnt antal på tredje plats kan vara 0, 2, 4, 6, dvs.. fyra siffror. Någon av de sju siffrorna kan komma på andra plats. Någon av sju siffror som inte är noll kan vara i första hand, dvs.. 6 möjligheter. Resultat = 4 * 7 * 6 = 168.
2. Hur många femsiffriga nummer finns det, som läser samma till vänster
höger och höger till vänster?
Vilket nummer som helst kan vara i första hand utom 0, dvs.. 9 möjligheter. Varje nummer kan vara på andra plats, dvs.. 10 möjligheter. Alla nummer från, dvs.. 10 möjligheter. Den fjärde och femte siffran är fördefinierade, de matchar första och andra, därmed, antalet sådana nummer är 9 * 10 * 10 = 900.
3. Det finns tio ämnen och fem lektioner per dag i klassen. På många sätt kan du
göra ett schema för en dag?
4. Hur många sätt du kan välja 4 delegera till konferensen, om i en grupp
20 man?

n = C₂₀4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)= 4845.

5. Hur många sätt kan åtta olika bokstäver sönderdelas i åtta
olika kuvert, om bara en bokstav läggs i varje kuvert?
Du kan lägga i det första kuvertet 1 med åtta bokstäver, i den andra av de sju som återstår, i den tredje av sex etc.. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Tre matematiker och tio ekonomer måste bestå av en kommission,
bestående av två matematiker och sex ekonomer. Hur många sätt är det
kan bli gjort?

Antal sätt att välja matematik C₃2= 3!/(2!*(3-2))!= 3/2, antal sätt att välja ekonom C₁₀6= 10!/(6!*(10-6))!= 7 * 8 * 9 * 10 /(1*2*3*4)= 210. n = C₃2*FRÅN₁₀6= 3 * 210 = 630.