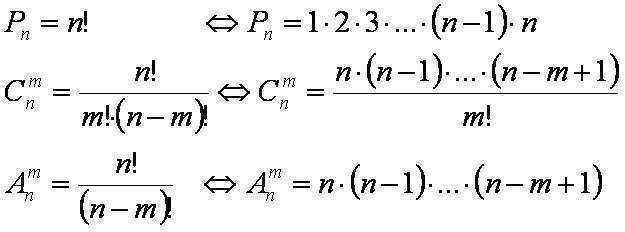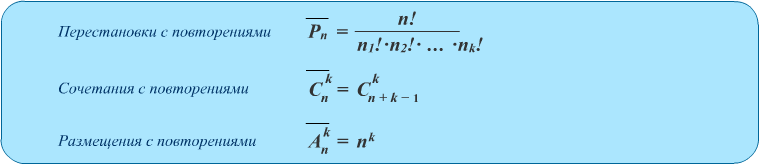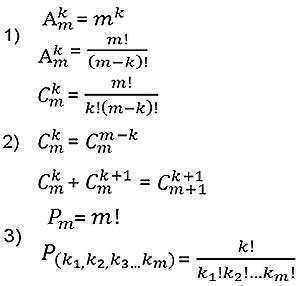องค์ประกอบ Combinatorial

ความมหัศจรรย์ของเงินในตัวเลข

ตัวเลขแต่ละตัวมีพลังงานของตัวเองและส่งผลต่อชีวิตของบุคคลในทางใดทางหนึ่ง. ตัวเลขของเงินช่วยกำหนดความหมายของตัวเลข, ค้นหารหัสส่วนตัวของเงินและความมั่งคั่ง. รหัสบัญชีคำนวณโดยใช้วันเดือนปีเกิด. จากนั้นคุณต้องดูการถอดเสียง. คุณต้องรู้ด้วย, วิธีใช้รหัสความมั่งคั่งของคุณอย่างถูกต้อง.

สิ่งสำคัญคือการคำนวณรหัสทางการเงินอย่างถูกต้อง

นอกจากนี้, อะไรคือจำนวนของความมั่งคั่ง, นอกจากนี้ยังมีตัวเลข, ไม่นำความอุดมสมบูรณ์มาสู่ชีวิตของบุคคล. พวกเขาจำเป็นต้องหลีกเลี่ยง. เพื่อดึงดูดกระแสการเงิน, ต้องทำความคุ้นเคยกับ, ตัวเลขแต่ละตัวหมายถึงอะไร:

1. ศูนย์และหนึ่ง. นักตัวเลขเชื่อว่า, ตัวเลขและรหัสเหล่านี้เป็นค่าลบสำหรับพลังงานทางการเงิน, พวกเขาจะไม่นำโชคดีมาให้. ดังนั้นคุณควรหลีกเลี่ยงการออม, เงินฝากด้วยจำนวนเงิน, ซึ่งมีตัวเลขเหล่านี้อยู่, เพราะจะทำให้กระแสเงินสดช้าลงและไม่นำมาซึ่งความมั่งคั่งและความสำเร็จ.
2. คู่. นี่เป็นรูปที่ไม่มีความสุข. เธอจะไม่นำความเจริญรุ่งเรืองและความสำเร็จ. ไม่แนะนำให้ใช้ธนบัตรของนิกายนี้เพื่อการออม, อย่าพกไว้ในกระเป๋าสตางค์ของคุณ.
3. สามคน. เป็นสิ่งที่ดีทางการเงิน, ด้วยความช่วยเหลือของผู้คนสามารถถูกลอตเตอรี่, หาแหล่งรายได้เพิ่มเติม. แต่นักตัวเลขไม่แนะนำให้สะสมเงิน, ผลรวมคือ 300, 3000, 30000. ตัวเลขนี้ต้องการการเคลื่อนไหวอย่างต่อเนื่อง, เธอต้องการพลังงาน, ไม่ใช่ความสงบ. สิ่งที่ดีที่สุดคือซื้อสลากกินแบ่งรัฐบาลในจำนวนดังกล่าวหรือลงทุนในธุรกิจของคุณเอง.
4. สี่ในรหัสส่วนบุคคลเป็นสัญลักษณ์ของความมั่นคง, ความน่าเชื่อถือ. เหมาะอย่างยิ่งสำหรับการออม, เงินออม, เงินลงทุนคือจำนวนตั๋วเงิน 400, 4000, 40000. ทางนี้, ความมั่งคั่งจะเพิ่มขึ้น.
5. ห้าเป็นรหัสตัวเลขที่สำคัญมากของความมั่งคั่งในตัวเลข. ตั๋วเงินที่มีหมายเลขนี้เป็นแม่เหล็กเงินจริง. พวกเขาสามารถยืมได้, ใช้จ่ายในการเดินทาง, สะสม, ใช้จ่าย, ตามที่คุณต้องการ.
6. รหัสทางการเงินดังกล่าวอาจเกี่ยวข้องกับข้อ จำกัด ทางการเงินบางประการ. ด้วยตัวเลขนี้ผู้คนเรียนรู้ที่จะประหยัด, ควบคุมการใช้จ่ายของคุณ. จำนวน 600, 6000 เป็นสัญลักษณ์ของความมั่นคงและความแน่นอน. นักตัวเลขไม่แนะนำให้ลงทุนในจำนวนดังกล่าว.
7. เซเว่นคือรหัส, โชคร้าย, ไม่สามารถใช้เป็นที่จัดเก็บได้, การลงทุน, เงินออม, เงินกู้และธุรกรรมทางการเงินอื่น ๆ, ซึ่งเกี่ยวข้องกับความเสี่ยง.
8. Eight เป็นรหัสความมั่งคั่งที่แข็งแกร่งในตัวเลข, เขาถือว่าประสบความสำเร็จมาก. เงินฝากสำหรับจำนวนเงิน 800, 8000, 80000 ประสบความสำเร็จอย่างมาก, ดึงดูดเงิน, เหมือนแม่เหล็ก.
9. เก้าเป็นสัญลักษณ์ของจิตวิญญาณและการพัฒนาภายใน. การหาเงินกับมันจะไม่เกิดขึ้น, แต่จะไม่มีการสูญเสียเช่นกัน. ขอแนะนำให้ใช้เงินจำนวนเก้าในการศึกษาด้วยตนเอง, การฝึกอบรม

เพื่อใช้ตัวเลขอย่างถูกต้อง, จำเป็นต้องรู้, วิธีคำนวณรหัสความมั่งคั่ง. ถัดไปคุณต้องหากฎสำหรับการใช้ชุดค่าผสมดังกล่าว. ฉันจะรวยไหม, ไม่เพียง แต่ขึ้นอยู่กับรหัสที่ได้รับจากการคำนวณเท่านั้น, แต่จากนั้นด้วย, วิธีใช้อย่างถูกต้อง.

ข้อมูลอ้างอิง

เอกสารรายงานโดยกล่าวถึงฐานเอกสารหลักทรัพย์บทบัญญัติเอกสารทางการเงินมติRubricator ตามหัวข้อการเงินเมืองของสหพันธรัฐรัสเซียตามวันที่ที่แน่นอนเงื่อนไขคำศัพท์ทางวิทยาศาสตร์การเงินเศรษฐกิจเวลาวันที่ 2015 2016 เอกสารในภาคการเงินในการลงทุน

ชุดค่าผสมที่ไม่มีการทำซ้ำ

งาน: ค้นหาชุดค่าผสมที่เป็นไปได้ทั้งหมดโดยไม่ต้องทำซ้ำจากหลายองค์ประกอบ {1,2,3} โดย 2.
มีชุดค่าผสมต่อไปนี้:1: 1 22: 1 33: 2 3
จำนวนชุดค่าผสมที่เป็นไปได้โดยไม่มีการซ้ำขององค์ประกอบ N โดย M สามารถกำหนดได้โดยสูตร (N≥M):

ที่อยู่ใน M! ครั้งน้อยกว่าจำนวนตำแหน่งที่เกี่ยวข้องโดยไม่มีการเกิดซ้ำ (เนื่องจากชุดค่าผสมที่ไม่มีการทำซ้ำไม่ได้ขึ้นอยู่กับลำดับขององค์ประกอบ).
พิจารณาปัญหาในการรับชุดค่าผสมทั้งหมดสำหรับหมายเลข 1 ... N โดย M. การใช้งานใน C ++

12345678910111213141516171819202122232425262728293031323334353637383940414243

#รวม <iostream>ใช้เนมสเปซมาตรฐาน;บูล NextSet(int * ก, int n, int ม){ int k = ม; สำหรับ (int ผม = k – 1; ผม >= 0; –ผม) ถ้า (ก < n – k + ผม + 1) { ++ก; สำหรับ (int j = i + 1; ญ < k; ++ญ) a = a + 1; กลับจริง; } กลับเท็จ;}เป็นโมฆะพิมพ์(int * ก, int n) { คง int num = 1; cout.width(3); ค่าใช้จ่าย << num ++ << “: “; สำหรับ (int ผม = 0; ผม < n; ผม ++) ค่าใช้จ่าย << ก << ” “; ค่าใช้จ่าย << endl;}int หลัก() { int n, ม, *ก; ค่าใช้จ่าย << “N = “; ประเทศจีน >> n; ค่าใช้จ่าย << “M = “; ประเทศจีน >> ม; a = int ใหม่; สำหรับ (int ผม = 0; ผม < n; ผม ++) a = i + 1; พิมพ์(ก, ม); ถ้า (n >= ม) { ในขณะที่ (NextSet(ก, n, ม)) พิมพ์(ก, ม); } cin.get(); cin.get(); กลับ 0;}

ผลการดำเนินการ

เลขศาสตร์ภาษาอังกฤษ: แนวคิดและสาระสำคัญ

ความรู้ที่เก่าแก่ที่สุด, ซึ่งช่วยอธิบาย, ตีความว่า, สิ่งที่เทวดาต้องการบอกมนุษย์, เรียกว่า angelic numerology.

จำ, ตัวเลขนั้นศึกษาการสั่นสะเทือนของตัวเลข, ตัวเลข, อิทธิพลที่มีต่อผู้คนและกระบวนการชีวิตของพวกเขา. นักคณิตศาสตร์ชาวอังกฤษอีกคน, นักโหราศาสตร์จอห์นดีในศตวรรษที่ 16 เขียนงานเกี่ยวกับตัวเลข, ซึ่งเขาถือว่าภาษาทูตสวรรค์สากลสำหรับการสื่อสารกับผู้คน.

ผู้ก่อตั้งการสอน Angelic Numerology ที่ค่อนข้างอายุน้อยคือ Doreen Verche. ทิพย์จากอเมริกา, นักจิตวิทยาและนักปรัชญา, ผู้เขียนหนังสือหลายเล่ม. เธออุทิศผลงานของเธอให้กับ Supreme Beings, รวมถึงเทพเจ้า, เทวดา, นักบุญ. เป็นเวลาหลายปีที่เธอค้นคว้าเกี่ยวกับปรากฏการณ์ที่ไม่สามารถอธิบายได้. แต่มันก็คุ้มค่า. เธอสร้างเครื่องดนตรี, ใครสามารถช่วยคุณตีความข้อความของผู้ช่วยของคุณจากสวรรค์. ตาม Doreen Verce, เราได้รับสัญญาณจากทูตสวรรค์เป็นประจำ, ซึ่งเตือนถึงอันตราย, แนะนำแนวทางแก้ไขปัญหาในชีวิตของบุคคล.

ทูตสวรรค์พูดคุยกับมนุษย์ด้วยตัวเลข, ตัวอักษร, สัญญาณ. ผลงานของ Doreen Verce พูดถึงเบาะแสจากผู้เฝ้าที่มองไม่เห็น, ซึ่งเข้ารหัสเป็นตัวเลขที่ซ้ำกันหรือรวมกัน. ได้แก่:

• บนป้ายทะเบียนรถยนต์;
• บนนาฬิกา;
• ในบราวนี่, อพาร์ทเม้น, เลขที่สำนักงาน;
• ในวันเดือนปีเกิด;
• ในรูปแบบตั๋ว, เช่นในการขนส่ง, และสิ่งอำนวยความสะดวกสาธารณะ ฯลฯ.

ในชุดค่าผสมดังกล่าวทั้งหมด, ตัวเลขซ่อนข้อมูล, ที่สามารถปรับเปลี่ยนอนาคตของผู้คน. Doreen Verce ได้ทำการวิจัยมากมายในหัวข้อนี้, ทุ่มเทให้กับการคำนวณตัวเลขตามวันเดือนปีเกิด. การคำนวณดังกล่าวช่วยในการระบุตัวเด็ก, ผู้มีความสามารถพิเศษตั้งแต่แรกเกิด, และไม่เพียงเท่านั้น.

จำนวนที่ตรงกัน, ชุดค่าผสมที่เรามักไม่สังเกตเห็น

แต่ก็คุ้มค่าที่จะให้ความสนใจ, เนื่องจากปรากฏการณ์ดังกล่าวอาจเป็นคำเตือนที่สำคัญ. ท้ายที่สุดทูตสวรรค์ไม่ได้ส่งสัญญาณดังกล่าวมาให้เราเพื่ออะไร

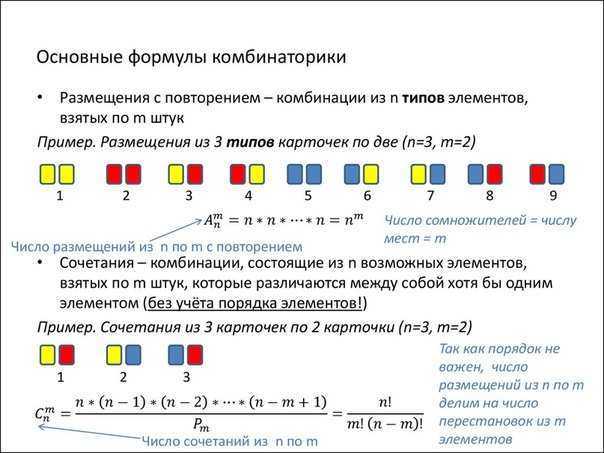
การผสมผสานกับการทำซ้ำ

การผสมผสานกับการทำซ้ำคือชุดขององค์ประกอบ M, ซึ่งแต่ละองค์ประกอบของเซต N สามารถเข้าร่วมได้หลายครั้ง. ในกรณีนี้ไม่มีการกำหนดข้อ จำกัด เกี่ยวกับอัตราส่วนของค่า M และ N, และจำนวนชุดค่าผสมทั้งหมดที่มีการทำซ้ำคือ

ตัวอย่างของปัญหาดังกล่าวคือการเลือกโปสการ์ด M จาก N ในทุกวิธีที่เป็นไปได้.

ในการสร้างชุดค่าผสมกับการทำซ้ำเราจะใช้วิธีแก้ปัญหาในการสร้างตำแหน่งด้วยการทำซ้ำ, พิจารณาการใช้งาน C ++

1234567891011121314151617181920212223242526272829303132333435363738394041

#รวม <iostream>ใช้เนมสเปซมาตรฐาน;บูล NextSet(int * ก, int n, int ม){ int j = ม – 1; ในขณะที่ (a == n && ญ >= 0) ญ–; ถ้า (ญ < 0) กลับเท็จ; ถ้า (ก >= n) ญ–; a ++; ถ้า (j == ม – 1) กลับจริง; สำหรับ (int k = j + 1; k < ม; k ++) a = a; กลับจริง;}เป็นโมฆะพิมพ์(int * ก, int n) { คง int num = 1; cout.width(3); ค่าใช้จ่าย << num ++ << “: “; สำหรับ (int ผม = 0; ผม < n; ผม ++) ค่าใช้จ่าย << ก << ” “; ค่าใช้จ่าย << endl;}int หลัก() { int n, ม, *ก; ค่าใช้จ่าย << “N = “; ประเทศจีน >> n; ค่าใช้จ่าย << “M = “; ประเทศจีน >> ม; int h = n > ม ? n : ม; // ขนาดของอาร์เรย์ a ถูกเลือกเป็นสูงสุด(n,ม) a = int ใหม่; สำหรับ (int ผม = 0; ผม < ซ; ผม ++) a = 1; พิมพ์(ก, ม); ในขณะที่ (NextSet(ก, n, ม)) พิมพ์(ก, ม); cin.get(); cin.get(); กลับ 0;}

ผลลัพธ์ของอัลกอริทึมข้างต้น:

อัลกอริทึม

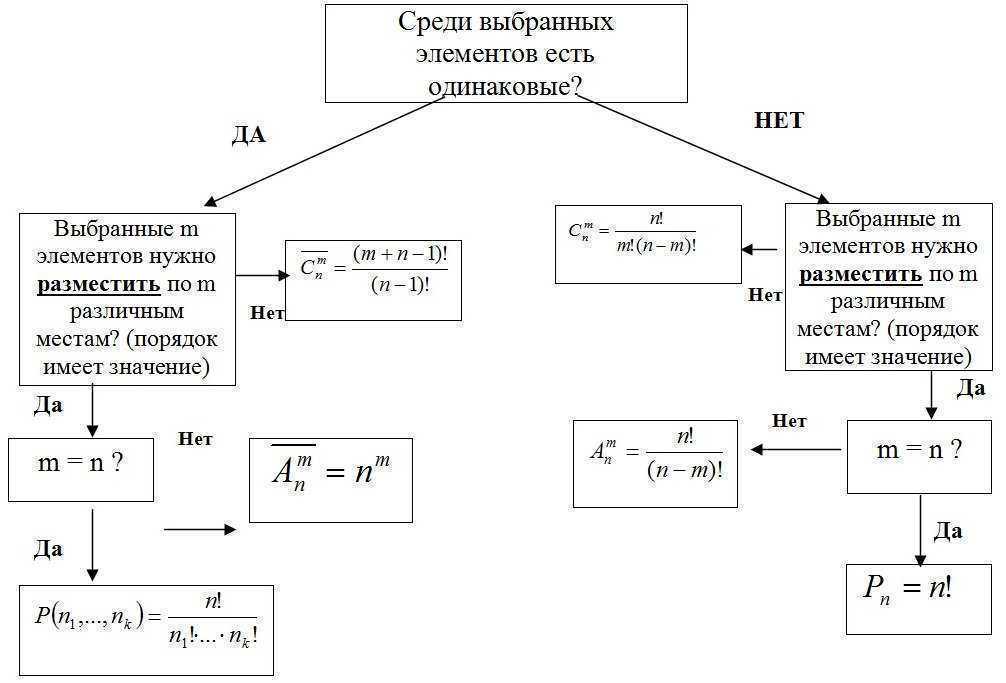
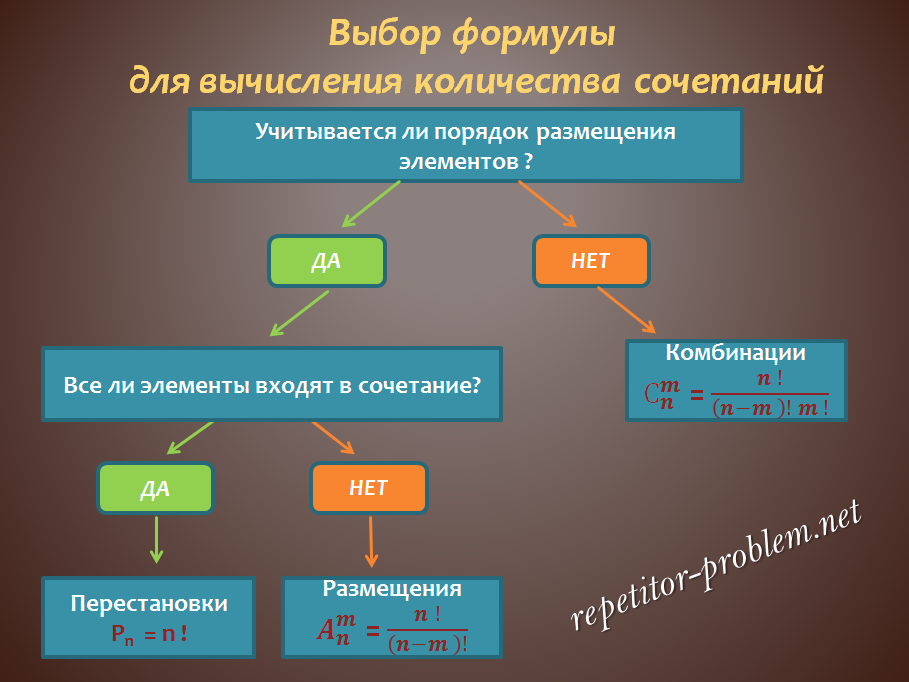
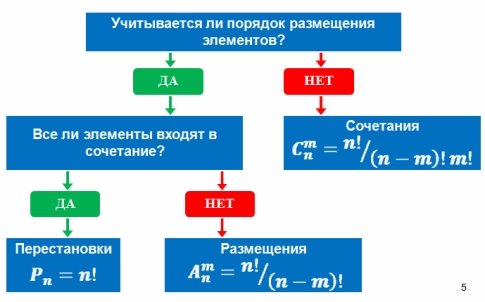
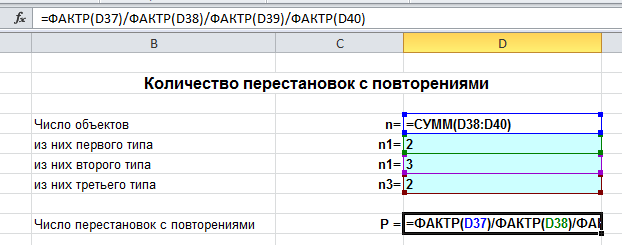
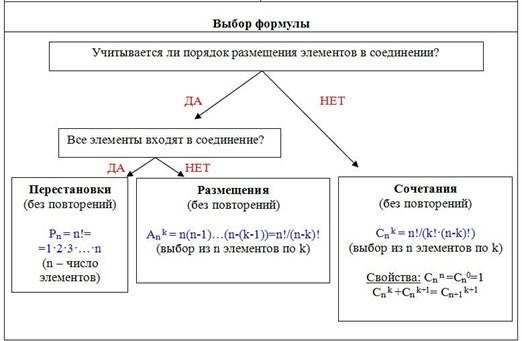
สูตรพื้นฐานของ Combinatorics

ให้มี k กลุ่มขององค์ประกอบ, และกลุ่ม i-th ประกอบด้วย n_ผม องค์ประกอบ.
เลือกหนึ่งองค์ประกอบจากแต่ละกลุ่ม. จากนั้นจำนวนทั้งหมด N ของวิธี,
ซึ่งสามารถเลือกได้, ถูกกำหนดโดยความสัมพันธ์ N = n₁*n₂*n₃*…*n_k.

ตัวอย่าง 1. ให้เราอธิบายกฎนี้ง่ายๆ
ตัวอย่าง. ให้มีสองกลุ่มขององค์ประกอบ, และกลุ่มแรกประกอบด้วย
n₁ องค์ประกอบ, และครั้งที่สอง – ของ n₂ องค์ประกอบ. เท่าไหร่
คู่ขององค์ประกอบที่แตกต่างกันสามารถประกอบด้วยสองกลุ่มนี้, ทางนี้,
เพื่อให้มีองค์ประกอบหนึ่งในคู่จากแต่ละกลุ่ม? ขอยอมรับ, เราเอา
องค์ประกอบแรกจากกลุ่มแรกและ, โดยไม่ต้องเปลี่ยนแปลง, เป็นไปได้ทั้งหมด
คู่รัก, เปลี่ยนเฉพาะองค์ประกอบจากกลุ่มที่สอง. คู่ดังกล่าวสำหรับองค์ประกอบนี้
สามารถเป็น n₂. จากนั้นเรานำรายการที่สองจากกลุ่มแรก
และยังเขียนคู่ที่เป็นไปได้ทั้งหมดสำหรับมัน. จะมี n คู่ดังกล่าวด้วย₂.
เนื่องจากกลุ่มแรกมีเพียง n₁ ธาตุ, เป็นไปได้ทั้งหมด
ตัวเลือกจะเป็น n₁*n₂.ตัวอย่าง 2. เท่าไหร่
เลขคู่สามหลักประกอบด้วยตัวเลข 0, 1, 2, 3, 4, 5, 6, ถ้า
ตัวเลขสามารถทำซ้ำได้?การตัดสินใจ: n₁= 6
(เพราะ. ในฐานะตัวเลขตัวแรกคุณสามารถนำตัวเลขใดก็ได้ 1, 2, 3, 4, 5, 6), n₂= 7
(เพราะ. ในฐานะตัวเลขหลักที่สองคุณสามารถนำตัวเลขใดก็ได้ 0, 1, 2, 3, 4, 5,
6), n₃= 4 (เพราะ. ในฐานะตัวเลขหลักที่สามคุณสามารถนำตัวเลขใดก็ได้ 0, 2, 4,
6).

ดังนั้น, N = n₁*n₂*n₃= 6 * 7 * 4 = 168.

ในกรณีนั้น, เมื่อทุกกลุ่มมีจำนวนองค์ประกอบเท่ากัน, กล่าวคือ. n₁= n₂=…n_k= n
ก็ถือว่าได้, ว่าทุกทางเลือกมาจากกลุ่มเดียวกัน, ยิ่งไปกว่านั้น
องค์ประกอบหลังจากการเลือกจะกลับไปที่กลุ่มอีกครั้ง. จากนั้นจำนวนวิธีทั้งหมด
ทางเลือกคือ nk. การเลือกประเภทนี้ใน Combinatorics เรียกว่าการเลือกที่มีผลตอบแทน.

ตัวอย่าง 3. ตัวเลขสี่หลักทั้งหมดเป็นกี่ตัว
สามารถประกอบด้วยตัวเลข 1, 5, 6, 7, 8?การตัดสินใจ. สำหรับทุกอันดับ
ตัวเลขสี่หลักมีความเป็นไปได้ห้าประการ, หมายถึง N = 5 * 5 * 5 * 5 = 54 = 625.

พิจารณาชุด, ประกอบด้วย n องค์ประกอบ. มัน
ชุดใน Combinatorics เรียกว่าทั่วไป
รวม.

ธุรกิจและการเงิน

ธนาคารความมั่งคั่งและสวัสดิการความเสียหาย(อาชญากรรม)การตลาดการจัดการการลงทุนหลักทรัพย์การจัดการ บริษัท ร่วมหุ้นสาธารณะโครงการเอกสารความปลอดภัย – ควบคุมหลักทรัพย์ – พันธบัตรการประเมินมูลค่าหนี้สกุลเงินอสังหาริมทรัพย์(เช่า)อาชีพงานการซื้อขายบริการการเงินประกันภัยงบประมาณบริการด้านการเงิน

จะทำอย่างไรกับรหัสมนต์หลังจากเสร็จสิ้นพิธีกรรม

หลังจาก, วิธีอ่านค่าตัวเลขระหว่าง 77 วัน, พวกเขาควรถูกเรียกเก็บเงินด้วย 4 องค์ประกอบสำหรับการทำงานต่อไป.

ในการทำเช่นนี้คุณต้องทำการปรับแต่งง่ายๆ:

1. เปิดใช้งานรหัสด้วยพลังงานของโลก. กระถางดินขนาดเล็กเหมาะสำหรับพิธีกรรม. คุณจะต้องมีเมล็ดพันธุ์ดอกไม้ด้วย. สิ่งเหล่านี้ควรเป็นเมล็ดพันธุ์, ไม่ใช่หน่อและหัวของพืช. หลังจากเตรียมแอตทริบิวต์ที่ต้องการ, ควรเขียนมนต์ลงบนกระดาษเปล่าและฝังไว้ในดิน, พูดคำสามครั้ง -“ โลกเต็มไปด้วยความมั่งคั่ง, ตอนนี้คุณคือความฝันของฉัน”. ถัดไปวางเมล็ดดอกไม้ลงในหม้อ.
2. หลังจากธาตุดินมนต์จะถูกชาร์จด้วยพลังงานของน้ำ. พิธีกรรมนี้ประกอบด้วยการรดน้ำเมล็ดพันธุ์, ซึ่งมาพร้อมกับคำว่า“ น้ำและดิน, ฟื้นเมล็ดพันธุ์”. เช่นเดียวกับในกรณีก่อนหน้านี้, แถลงการณ์ 3 ครั้ง.
3. ถัดไปมาถึงการเปลี่ยนองค์ประกอบของ Air. ควรนำหม้อที่มีพืชในอนาคตไปเปิดหน้าต่างและพูดว่า: "คุณ, แอร์, ฉันต้องการ, เหมือนแสง, และให้รุ่งอรุณแห่งความฝันของฉัน ". จะต้องทำซ้ำภายใน 3 วัน.
4. เมื่อเมล็ดงอกปรากฏขึ้น, ถึงเวลาสำหรับองค์ประกอบของไฟ. ต้องจุดเทียนใหม่เพื่อปลุกมนต์. จะต้องวางไว้ข้างๆต้นไม้และ, มีสมาธิ, พูดสามครั้ง: “ มันกำลังไหม้, ไฟ, เทียน - เผาไหม้, และทำลายความยากจน. ปล่อยให้ถั่วงอกเจริญเติบโต, สลิปเงินซ่อนอะไรอยู่. และเราจะเจริญรุ่งเรืองไปพร้อมกับเขา, ดึงดูดความมั่งคั่งด้วยเงิน ".

หลังจากขั้นตอนเหล่านี้รหัสสกุลเงินจะเริ่มทำงาน. ไม่แนะนำให้ทิ้งหม้อพร้อมกับต้นกล้าและมนต์, ดูแลพืชตามปกติต่อไป.

นอกจากนี้, เพื่อเพิ่มผลของรหัสมนต์, คุณสามารถใช้ภาพตัวเลขบนแผ่นกระดาษแข็งโดยใช้หมึกสีเขียวและสีแดง. เครื่องรางเงินดังกล่าวจะต้องพกติดตัวตลอดเวลา.

ความมหัศจรรย์ของสิ่งที่คุ้นเคย

เครื่องกำเนิดตัวเลขสุ่มสุ่มออนไลน์ของเรา.

โปรแกรมสร้าง Randomizer ของเราไม่จำเป็นต้องดาวน์โหลดลงในพีซีส่วนตัวของคุณ. ทุกอย่างเกิดขึ้นในโหมดสร้างหมายเลขออนไลน์. เพียงระบุพารามิเตอร์เหล่านี้, เช่น: ช่วงของตัวเลขออนไลน์, โดยจะสุ่มเลือกตัวเลข. ระบุจำนวนตัวเลขด้วย, ซึ่งจะถูกเลือก.
ตัวอย่างเช่น, คุณมีกลุ่ม Vkontakte. ในกลุ่มคุณแสดงออก 5 รางวัล, ในหมู่ผู้เข้าร่วม, ใครจะโพสต์บันทึกใหม่. ใช้แอพเฉพาะ, เรามีรายชื่อผู้เข้าร่วม. แต่ละคนได้รับการกำหนดหมายเลขลำดับสำหรับหมายเลขออนไลน์.

ตอนนี้ไปที่ตัวสร้างออนไลน์ของเราและระบุช่วงของตัวเลข (จำนวนผู้เข้าร่วม). ตัวอย่างเช่น, ถาม, เลขออนไลน์ต้องการอะไร 5, ตั้งแต่เรามี 5 รางวัล. ตอนนี้กดปุ่มสร้าง. จากนั้นเราจะได้รับ 5 สุ่มตัวเลขออนไลน์, ตั้งแต่ 1 ถึง 112 รวม. สร้างแล้ว 5 หมายเลขออนไลน์จะตรงกับหมายเลขประจำเครื่องของผู้เข้าร่วมห้าคน, ซึ่งกลายเป็นผู้ชนะการวาดภาพ. ทุกอย่างง่ายและสะดวก.

ข้อดีอีกอย่างของตัวสร้างตัวเลขสุ่มคือ, ตัวเลขทั้งหมดทางออนไลน์จะได้รับแบบสุ่ม. นั่นคือมีอิทธิพลต่อเขา, หรือคำนวณ, จะเป็นเลขอะไรต่อไป, ดูเหมือนจะเป็นไปไม่ได้. สิ่งที่เครื่องกำเนิดไฟฟ้าสามารถพูดได้, ซื่อสัตย์และเชื่อถือได้, และการบริหาร, ซึ่งแจกรางวัลโดยใช้เครื่องกำเนิดไฟฟ้าฟรีของเรา, ซื่อสัตย์และดีต่อหน้าผู้เข้าร่วมการแข่งขัน. และหากคุณมีข้อสงสัยเกี่ยวกับวิธีแก้ปัญหา, จากนั้นคุณสามารถใช้ตัวสร้างคำตอบใช่หรือไม่ใช่ของเรา.

วิธีคำนวณรหัสความมั่งคั่งของคุณ

มีดีและไม่ดีรวมกัน

ตัวเลขและเงินมีความสัมพันธ์กันอย่างใกล้ชิด. มีการผสมตัวเลข, สร้างความมั่งคั่ง, แต่มีชุดค่าผสมที่ไม่สำเร็จ. หากคุณใช้อย่างถูกต้อง, ความสำเร็จและโชคจะอยู่เคียงข้างคุณ. การคำนวณรหัสเป็นเรื่องง่าย. ในการดำเนินการนี้คุณต้องทำการคำนวณต่อไปนี้:

• เขียนหมายเลขของคุณลงบนกระดาษเปล่า, เดือนและปีเกิด (เช่น, 31.10.1987);
• เพื่อคำนวณมูลค่าความสำเร็จ, ควรเพิ่มสองหลักแรก, เช่น, วันเดือนปีเกิดที่เฉพาะเจาะจง (เช่น, 31 - 3 + 1 = 4). หมายเลขนี้จะเป็นหมายเลขแรกในชุดค่าผสม;
• เพื่อคำนวณอักขระที่สองของชุดค่าผสม, จำเป็นต้องคำนวณมูลค่าของเดือน (เช่น, ตุลาคม, 10 เดือน - 1 + 0 = 1);
• ตอนนี้คุณต้องคำนวณจำนวนปีเกิด (เช่น, 1987 - 1 + 9 + 8 + 7 = 25, 2+5= 7);
• ในตอนท้ายคุณต้องคำนวณอักขระสุดท้ายของชุดค่าผสมเป็นการส่วนตัว, สำหรับสิ่งนี้ทั้งสามหมายเลขที่ได้รับก่อนหน้านี้จะถูกสรุป (เช่น, 4+1+7= 12, 1+2= 3, ในกรณีนี้การรวมเงินคือ 4173). ชุดค่าผสมที่ได้คือรหัสส่วนบุคคลสำหรับบุคคล.

นอกเหนือจากรหัสส่วนตัว, มีค่าสากล, ที่ทุกคนสามารถนำไปใช้ได้, เหมือนเศรษฐี, และมีรายได้ปานกลาง. นี่คือมาสคอตดิจิทัล, ซึ่งแสดงในรูปแบบของสี่แปดที่มีขนาดเท่ากัน. การรวมกันนี้มีความแข็งแกร่งมาก, หมายถึงความสำเร็จและความมั่นคงทางการเงิน.

คุณยังสามารถคำนวณได้, ฉันจะรวยไหม, โดยชื่อ. สำหรับสิ่งนี้จะมีการใช้ตารางความสอดคล้องระหว่างตัวอักษรและตัวเลข. ตัวอย่างเช่น, ท่าจอดเรือ, ซึ่งเกิด 5 ตัวเลข. ในกรณีนี้จะถ่ายเฉพาะวันเกิดเท่านั้น:

M-5, ก -1, ร -9, I-1, N-6, ก -1. 5+1+9+1+6+1= 23, 2+3= 5. จากนั้นเพิ่มวันเดือนปีเกิด - 5 + 5 = 10, 1+0= 1 - หนึ่งและเป็นรหัสแห่งโชคและเงินสำหรับบุคคลใดบุคคลหนึ่ง. แต่เขาจะประสบความสำเร็จได้ไหม, ขึ้นอยู่กับ, ใช้ดีแค่ไหน.

การเรียงลำดับขององค์ประกอบ n

คำจำกัดความ 3. การเรียงสับเปลี่ยน
ของ n องค์ประกอบ
เรียกชุดที่สั่งซื้อ
องค์ประกอบเหล่านี้.

ตัวอย่างที่ 7 ก. การเรียงสับเปลี่ยนทุกชนิด
จำนวนมาก, ประกอบด้วยสามองค์ประกอบ {1, 2, 3} คือ: (1, 2, 3), (1, 3,
2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

จำนวนการเรียงสับเปลี่ยนที่แตกต่างกันขององค์ประกอบ n แสดงโดย P_n และ
คำนวณโดยสูตร P_n= n!.

ตัวอย่าง 8. หนังสือเจ็ดเล่มมีกี่วิธี
ผู้เขียนที่แตกต่างกันสามารถจัดเรียงเป็นแถวเดียวบนชั้นวาง?การตัดสินใจ:ปัญหานี้เกี่ยวกับจำนวน
จัดเรียงหนังสือเจ็ดเล่มใหม่. มี P₇= 7!= 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040
วิธีจัดเรียงหนังสือ.

อภิปรายผล. ที่เราเห็น,
สามารถคำนวณจำนวนชุดค่าผสมที่เป็นไปได้ตามกฎต่างๆ
(การเรียงสับเปลี่ยน, ชุดค่าผสม, ตำแหน่ง) และผลลัพธ์จะแตกต่างกัน,
เพราะ. หลักการนับและสูตรนั้นแตกต่างกัน. มองอย่างใกล้ชิดที่
คำจำกัดความ, สามารถมองเห็นได้, ผลลัพธ์นั้นขึ้นอยู่กับปัจจัยหลายประการ
ในเวลาเดียวกัน.
ในตอนแรก, จากนั้น, จากจำนวนองค์ประกอบที่เราสามารถรวมเข้าด้วยกัน
ชุด (จำนวนองค์ประกอบทั้งหมดมีขนาดใหญ่เพียงใด).
ประการที่สอง, ผลลัพธ์ขึ้นอยู่กับ, ชุดขององค์ประกอบสำหรับเรามีขนาดใหญ่เพียงใด
ความต้องการ

และสุดท้าย, สิ่งสำคัญคือต้องรู้, สำหรับเรา
ลำดับรายการที่จำเป็นในชุด. ให้เราอธิบายปัจจัยสุดท้ายใน
ตัวอย่างต่อไปนี้

ตัวอย่าง 9. ในการประชุมผู้ปกครอง
นำเสนอ 20 ชาย. ตัวเลือกการจัดองค์ประกอบมีกี่แบบ
คณะกรรมการผู้ปกครอง, ถ้ามันควรจะเข้า 5 ชาย?การตัดสินใจ: ในตัวอย่างนี้เรา
ไม่สนใจลำดับรายชื่อในรายชื่อคณะกรรมการ. หากเป็นผลให้ในไฟล์
องค์ประกอบจะเป็นคนเดียวกัน, แล้วความหมายสำหรับเราก็เหมือนกัน
ตัวเลือก. ดังนั้นเราสามารถใช้สูตรคำนวณจำนวนชุดค่าผสมจาก 20 องค์ประกอบโดย 5.
สิ่งต่างๆจะแตกต่างกันออกไป, หากกรรมการแต่ละคนรับผิดชอบในเบื้องต้น
ทิศทางการทำงานที่ชัดเจน. จากนั้นด้วยบัญชีเงินเดือนเดียวกัน
คณะกรรมการ, ข้างในเป็นไปได้ 5! ตัวเลือกการเปลี่ยนแปลง, เรื่องไหน. จำนวน
แตกต่างกัน (และองค์ประกอบ, และตามพื้นที่รับผิดชอบ) ตัวเลือกที่กำหนดไว้ใน
ในกรณีนี้จำนวนตำแหน่ง
ของ 20 องค์ประกอบโดย 5.

งานทดสอบตัวเอง
1. เลขคู่สามหลักสามารถสร้างจากตัวเลขได้กี่หลัก 0, 1, 2, 3, 4, 5,
6, ถ้าตัวเลขสามารถทำซ้ำได้?
ตั้งแต่. เลขคู่ในอันดับที่สามได้ 0, 2, 4, 6, กล่าวคือ. สี่หลัก. ตัวเลขเจ็ดหลักใด ๆ สามารถอยู่ในอันดับที่สองได้. ตัวเลขเจ็ดหลักใด ๆ ที่ไม่ใช่ศูนย์สามารถอยู่ในอันดับแรกได้, กล่าวคือ. 6 โอกาส. ผลลัพธ์ = 4 * 7 * 6 = 168.
2. ตัวเลขห้าหลักมีกี่ตัว, ซึ่งอ่านเหมือนกันทางด้านซ้าย
ขวาและขวาไปซ้าย?
หมายเลขใดก็ได้ในอันดับแรกยกเว้น 0, กล่าวคือ. 9 โอกาส. หมายเลขใดก็ได้ในอันดับที่สอง, กล่าวคือ. 10 โอกาส. หมายเลขใดก็ได้จาก, กล่าวคือ. 10 โอกาส. ตัวเลขที่สี่และห้าถูกกำหนดไว้ล่วงหน้า, ตรงกับครั้งแรกและครั้งที่สอง, ด้วยเหตุนี้, จำนวนของตัวเลขดังกล่าวคือ 9 * 10 * 10 = 900.
3. ในชั้นเรียนมีสิบวิชาและห้าบทเรียนต่อวัน. คุณสามารถทำได้หลายวิธี
กำหนดตารางเวลาสำหรับหนึ่งวัน?
4. คุณสามารถเลือกได้กี่วิธี 4 มอบหมายให้เข้าร่วมการประชุม, ถ้าอยู่ในกลุ่ม
20 ชาย?

n = ค₂₀4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)= 4845.

5. แปดตัวอักษรที่แตกต่างกันสามารถย่อยสลายเป็นแปดได้กี่วิธี
ซองจดหมายต่างๆ, หากใส่จดหมายเพียงฉบับเดียวในแต่ละซอง?
ใส่ซองแรกก็ได้ค่ะ 1 แปดตัวอักษร, ในหนึ่งวินาทีในเจ็ดที่เหลือ, ในสามหนึ่งในหกเป็นต้น. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. นักคณิตศาสตร์สามคนและนักเศรษฐศาสตร์สิบคนจะต้องประกอบด้วยคณะกรรมการ,
ประกอบด้วยนักคณิตศาสตร์สองคนและนักเศรษฐศาสตร์หกคน. มันมีกี่วิธี
สามารถทำได้?

จำนวนวิธีในการเลือกคณิตศาสตร์ค₃2= 3!/(2!*(3-2))!= 3/2, หลายวิธีในการเลือกนักเศรษฐศาสตร์ค₁₀6= 10!/(6!*(10-6))!= 7 * 8 * 9 * 10 /(1*2*3*4)= 210. n = ค₃2*จาก₁₀6= 3 * 210 = 630.