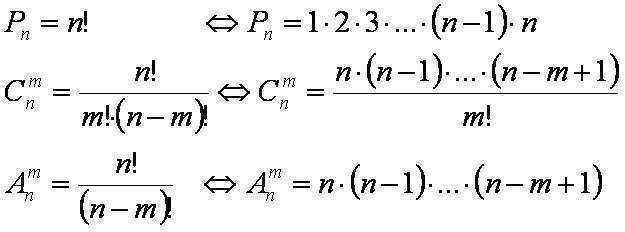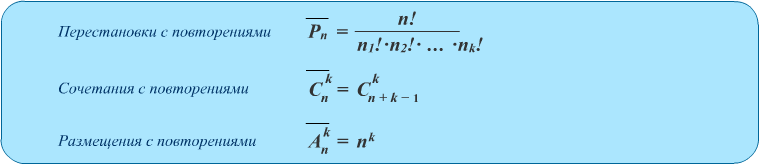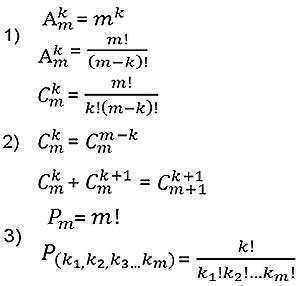Các yếu tố kết hợp

Sự kỳ diệu của tiền trong số học

Mỗi con số có năng lượng riêng của nó và ảnh hưởng đến cuộc sống của một người theo một cách nhất định.. Số học của tiền giúp xác định ý nghĩa của một con số, tìm ra mã cá nhân của tiền bạc và sự giàu có. Mã tài chính được tính theo ngày tháng năm sinh. Sau đó, bạn cần xem bảng điểm. Bạn cũng cần biết, cách sử dụng mã tài sản của bạn một cách chính xác.

Điều chính là tính toán chính xác mã tài chính

ngoài ra, số của cải là bao nhiêu, cũng có những con số, không mang lại sự phong phú cho cuộc sống của một người. Chúng cần được tránh. Để thu hút dòng tài chính, cần phải tự làm quen với, mỗi số viết tắt cho cái gì:

1. Không và một. Các nhà số học tin rằng, rằng những con số và mã này là tiêu cực cho năng lượng tiền tệ, chúng sẽ không mang lại may mắn. Vì vậy, bạn nên tránh tiết kiệm., tiền gửi với số tiền, trong đó những con số này hiện diện, bởi vì chúng sẽ làm chậm dòng tiền và không mang lại sự thịnh vượng và thành công.
2. Cặp đôi. Đây là một con số không vui. Cô ấy sẽ không mang lại sự thịnh vượng và thành công. Không nên sử dụng tiền giấy mệnh giá này để tiết kiệm, đừng mang chúng trong ví của bạn.
3. Chơi ba người. Có thuận lợi về tài chính không, với sự giúp đỡ của nó, một người có thể thắng xổ số, tìm thêm nguồn thu nhập. Nhưng các nhà số học không khuyên bạn nên tích lũy tiền., tổng của nó là 300, 3000, 30000. Con số này cần chuyển động liên tục, cô ấy cần năng lượng, không hòa bình. Điều tốt nhất là mua một vé số với số tiền như vậy hoặc đầu tư vào công việc kinh doanh của riêng bạn..
4. Bốn trong mã cá nhân là biểu tượng của sự ổn định, độ tin cậy. Lý tưởng để tiết kiệm, tiết kiệm, đầu tư là số lượng hóa đơn 400, 4000, 40000. Theo cách này, sự giàu có sẽ tăng lên.
5. Năm là một mã số rất quan trọng của sự giàu có trong số học. Hóa đơn có số này là nam châm tiền thật.. Họ có thể được cho vay, chi tiêu cho du lịch, tích trữ, tiêu như vậy, như bạn thích.
6. Mã tài chính như vậy có thể thu hút một số hạn chế tài chính nhất định. Với con số này, mọi người học cách tiết kiệm, kiểm soát chi tiêu của bạn. Lượng 600, 6000 là biểu tượng của sự ổn định và chắc chắn. Các nhà số học không khuyên bạn nên đầu tư số tiền như vậy.
7. Bảy là mã, xui xẻo, nó không thể được sử dụng để lưu trữ, đầu tư, tiết kiệm, các khoản vay và bất kỳ giao dịch tài chính nào khác, có liên quan đến rủi ro.
8. Tám là một mã giàu có mạnh mẽ trong số học, anh ấy được coi là rất thành công. Đặt cọc cho số tiền 800, 8000, 80000 rất thành công, họ thu hút tiền, như một nam châm.
9. Chín là biểu tượng của tâm linh và sự phát triển nội tâm. Việc huy động tiền bằng nó sẽ không xảy ra, nhưng cũng sẽ không mất mát. Nên dành số tiền bằng điểm chín cho việc tự học, đào tạo

Để sử dụng số một cách chính xác, cần phải biết, cách tính mã tài sản. Tiếp theo, bạn cần tìm ra quy tắc sử dụng kết hợp như vậy.. Tôi sẽ trở nên giàu có, không chỉ phụ thuộc vào mã thu được do kết quả của phép tính, nhưng cũng từ đó, làm thế nào để sử dụng nó một cách chính xác.

Tài liệu tham khảo

Tài liệuLawsThông báoTài liệuĐiều khoảnĐiều khoản tham chiếuKế hoạch phát triểnKhoa học tài liệuPhân tíchEventsContestsTổng sốQuản trị các thành phốĐơn đặt hàngCông việcGiao thức công việcCác dự án đấu giáCác dự ánCông cụBáo cáobằng cách đề cập Cơ sở tài liệu Chứng khoánĐiều khoảnTài liệu tài chínhQuyết tâmCông cụ chấm điểm theo chủ đề Tài chính Các thành phố của Liên bang Nga Khu vực theo ngày chính xácĐiều kiệnThuật ngữ khoa học Kinh tế tài chínhThời gianNgày 2015 2016 Các tài liệu trong lĩnh vực tài chính đầu tư

Kết hợp không lặp lại

Một nhiệm vụ: Tìm tất cả các kết hợp có thể có mà không có sự lặp lại từ nhiều phần tử {1,2,3} bởi 2.
Các kết hợp sau tồn tại:1: 1 22: 1 33: 2 3
Số lượng các tổ hợp có thể có mà không có sự lặp lại của N phần tử của M có thể được xác định bằng công thức (N≥M):

cái đó ở M! ít hơn lần so với số lượng vị trí tương ứng không có lặp lại (vì các kết hợp không lặp lại không phụ thuộc vào thứ tự của các phần tử).
Xem xét vấn đề lấy tất cả các kết hợp cho các số 1 ... N bằng M. Thực hiện trong C ++

12345678910111213141516171819202122232425262728293031323334353637383940414243

#bao gồm <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int k = m; cho (int i = k – 1; Tôi >= 0; –Tôi) nếu (a < n – k + Tôi + 1) { ++a; cho (int j = i + 1; j < k; ++j) a = a + 1; return true; } trả về sai;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; cho (int i = 0; Tôi < n; i++) cout << a << ” “; cout << endl;}int main() { int n, m, *a; cout << “N = “; cin >> n; cout << “M = “; cin >> m; a = new int; cho (int i = 0; Tôi < n; i++) a = i + 1; Print(a, m); nếu (n >= m) { trong khi (NextSet(a, n, m)) Print(a, m); } cin.get(); cin.get(); trở về 0;}

Результат выполнения

Số học tiếng anh: khái niệm và bản chất

Kiến thức lâu đời nhất, giúp giải thích, giải thích điều đó, những gì thiên thần muốn nói với con người, được gọi là thiên thần số học.

Gợi lại, số học nghiên cứu sự dao động của các con số, chữ số, ảnh hưởng của họ đối với con người và quá trình sống của họ. Một nhà toán học người Anh khác, nhà chiêm tinh học John Dee vào thế kỷ 16 đã viết một tác phẩm về các con số, mà anh ấy coi là ngôn ngữ thiên thần phổ quát để giao tiếp với mọi người.

Người sáng lập ra phương pháp giảng dạy tương đối trẻ về Thần số học là Doreen Verche. Clairvoyant từ Mỹ, nhà tâm lý học và triết học, tác giả của nhiều cuốn sách. Cô ấy đã cống hiến những tác phẩm của mình cho những Đấng Tối cao, bao gồm các vị thần, thiên thần, thánh. Trong nhiều năm, cô đã nghiên cứu các hiện tượng không giải thích được.. Nhưng nó đáng mà. Cô ấy đã tạo ra nhạc cụ, ai có thể giúp bạn giải thích thông điệp của những người giúp đỡ bạn từ thiên đàng. Theo Doreen Verce, chúng tôi thường xuyên nhận được dấu hiệu từ các thiên thần, cảnh báo nguy hiểm, đề xuất giải pháp cho các vấn đề trong cuộc sống của một người.

Thiên thần nói chuyện với con người bằng những con số, bức thư, dấu hiệu. Các tác phẩm của Doreen Verce nói về manh mối từ những kẻ canh giữ vô hình, được mã hóa bằng các chữ số lặp lại hoặc kết hợp của chúng. Cụ thể:

• trên biển số ô tô;
• trên đồng hồ;
• trong bánh hạnh nhân, căn hộ, chung cư, đánh số văn phòng;
• trong ngày sinh;
• ở dạng vé, như trong giao thông vận tải, và các cơ sở công cộng, v.v..

Trong tất cả các kết hợp như vậy, số liệu ẩn dữ liệu, ai có thể điều chỉnh tương lai của con người. Doreen Verce đã thực hiện rất nhiều nghiên cứu về chủ đề này, dành riêng cho các phép tính số học theo ngày sinh. Tính toán như vậy giúp xác định trẻ em., người có khả năng độc đáo từ khi sinh ra, và không chỉ.

Số trận đấu, sự kết hợp chúng tôi thường không nhận thấy

Nhưng nó đáng chú ý, bởi vì một hiện tượng như vậy có thể là một cảnh báo quan trọng. Rốt cuộc, các thiên thần không gửi cho chúng ta một dấu hiệu như vậy để làm gì

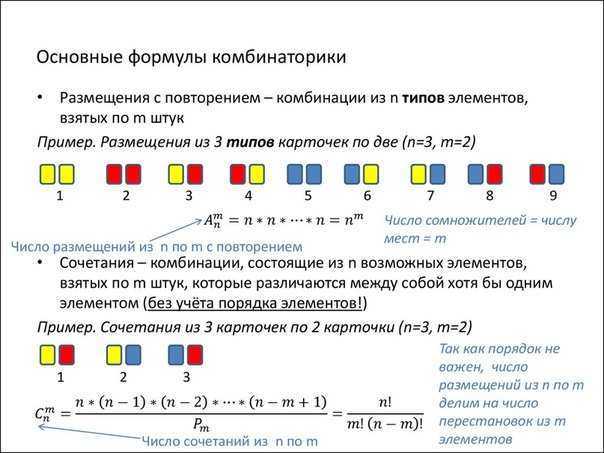
Kết hợp với lặp lại

Các tổ hợp có lặp lại là tập hợp M phần tử, trong đó mỗi phần tử của tập N có thể tham gia nhiều lần. Trong trường hợp này, không có hạn chế nào được áp dụng đối với tỷ lệ giữa các giá trị của M và N, và tổng số kết hợp có số lần lặp lại là

Một ví dụ của một vấn đề như vậy là sự lựa chọn M bưu thiếp từ N theo tất cả các cách có thể.

Để tạo các kết hợp có số lần lặp lại, chúng tôi sẽ sử dụng giải pháp tạo các vị trí có số lần lặp lại., được xem xét. Triển khai C ++

1234567891011121314151617181920212223242526272829303132333435363738394041

#bao gồm <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int j = m – 1; trong khi (a == n && j >= 0) j–; nếu (j < 0) trả về sai; nếu (a >= n) j–; a++; nếu (j == m – 1) return true; cho (int k = j + 1; k < m; k++) a = a; return true;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; cho (int i = 0; Tôi < n; i++) cout << a << ” “; cout << endl;}int main() { int n, m, *a; cout << “N = “; cin >> n; cout << “M = “; cin >> m; int h = n > m ? n : m; // размер массива а выбирается как max(n,m) a = new int; cho (int i = 0; Tôi < h; i++) a = 1; Print(a, m); trong khi (NextSet(a, n, m)) Print(a, m); cin.get(); cin.get(); trở về 0;}

Kết quả của thuật toán trên:

Thuật toán

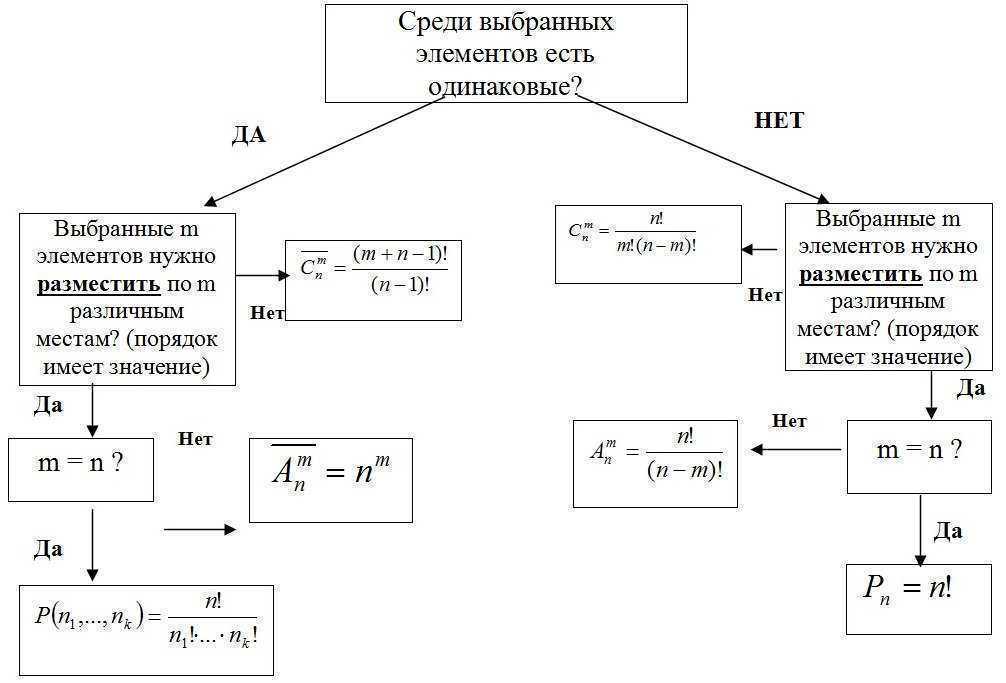
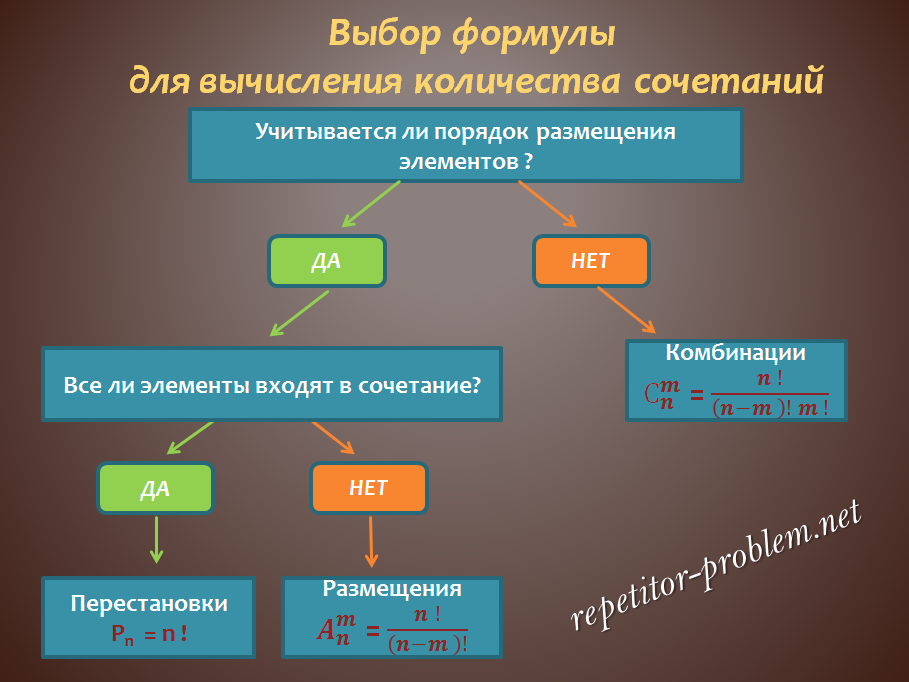
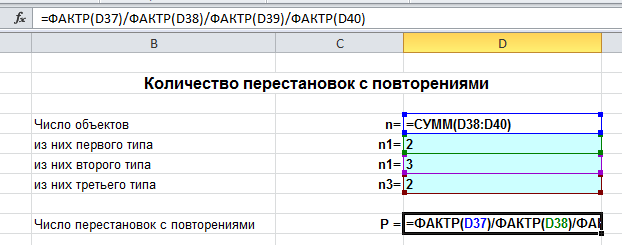
Công thức cơ bản của tổ hợp

Cho có k nhóm phần tử, và nhóm thứ i gồm n_Tôi các yếu tố.
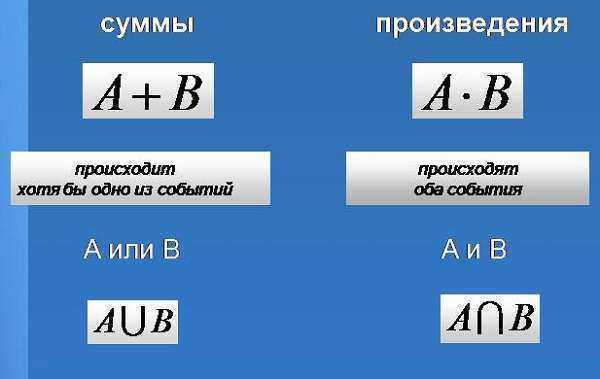
Chọn một phần tử từ mỗi nhóm. Khi đó tổng số N cách,
với một sự lựa chọn như vậy có thể được thực hiện, được xác định bởi quan hệ N = n₁*n₂*n₃*…*n_k.

Thí dụ 1. Hãy để chúng tôi giải thích quy tắc này một cách đơn giản
thí dụ. Giả sử có hai nhóm phần tử, và nhóm đầu tiên bao gồm
n₁ các yếu tố, va thu hai – của n₂ các yếu tố. bao nhiêu
các cặp phần tử khác nhau có thể được tạo thành từ hai nhóm này, theo cách này,
để có một phần tử trong một cặp từ mỗi nhóm? Hãy thừa nhận, Chúng tôi đã lấy
phần tử đầu tiên từ nhóm đầu tiên và, mà không cần thay đổi nó, đã vượt qua tất cả những gì có thể
các cặp đôi, chỉ thay đổi các phần tử từ nhóm thứ hai. Các cặp như vậy cho phần tử này
có thể là n₂. Sau đó, chúng tôi lấy mục thứ hai từ nhóm đầu tiên
và cũng soạn tất cả các cặp có thể có cho nó. Cũng sẽ có n cặp như vậy₂.
Vì nhóm đầu tiên chỉ chứa n₁ thành phần, tất cả có thể
lựa chọn sẽ là n₁*n₂.Thí dụ 2. bao nhiêu
số chẵn có ba chữ số có thể bao gồm các chữ số 0, 1, 2, 3, 4, 5, 6, nếu
số có thể được lặp lại?Phán quyết: n₁= 6
(bởi vì. là chữ số đầu tiên, bạn có thể lấy bất kỳ chữ số nào từ 1, 2, 3, 4, 5, 6), n₂= 7
(bởi vì. là chữ số thứ hai, bạn có thể lấy bất kỳ chữ số nào từ 0, 1, 2, 3, 4, 5,
6), n₃= 4 (bởi vì. là chữ số thứ ba, bạn có thể lấy bất kỳ chữ số nào từ 0, 2, 4,
6).

vì thế, N = n₁*n₂*n₃= 6 * 7 * 4 = 168.

Trong trường hợp đó, khi tất cả các nhóm có cùng số phần tử, I E. n₁= n₂=…n_k= n
nó có thể được coi là, rằng mọi lựa chọn đều được thực hiện từ cùng một nhóm, hơn thế nữa
phần tử sau khi chọn trở lại nhóm một lần nữa. Sau đó, số tất cả các cách
lựa chọn là nk. Loại lựa chọn này trong tổ hợp được gọi là lựa chọn có trả về.

Thí dụ 3. Có bao nhiêu số có bốn chữ số
có thể được tạo thành từ các con số 1, 5, 6, 7, 8?Phán quyết. Cho mọi thứ hạng
một số có bốn chữ số có năm khả năng, nghĩa là N = 5 * 5 * 5 * 5 = 54 = 625.

Xem xét bộ, gồm n phần tử. nó
một tập hợp trong tổ hợp được gọi là tổng quát
tổng hợp.

Kinh doanh và tài chính

Ngân hàngSức khỏe và Phúc lợi(Tội ác)Tiếp thịQuản lýĐầu tư Chứng khoánQuản lýCông ty cổ phần đại chúng Dự ánTài liệu Chứng khoán – kiểm soát chứng khoán – Định giá Trái phiếu Nợ Tiền tệ Bất động sản(Thuê)Nghề nghiệpJobsTradingServicesFinanceInsuranceBudgetDịch vụ tài chính

Làm gì với mã thần chú sau khi hoàn thành nghi lễ

Sau, cách các giá trị số được đọc trong 77 ngày, họ nên bị tính phí 4 các yếu tố cho công việc tiếp theo.

Để thực hiện, bạn cần thực hiện các thao tác đơn giản.:

1. Kích hoạt mã bằng năng lượng của Trái đất. Một chậu đất nhỏ thích hợp cho nghi lễ.. Bạn cũng sẽ cần bất kỳ hạt giống hoa nào. Đây chính xác là những hạt giống., không phải chồi và củ của cây. Sau khi chuẩn bị các thuộc tính cần thiết, câu thần chú nên được viết trên một mảnh giấy trắng và chôn xuống đất, nói những từ đó ba lần - "Trái đất đầy giầu có, bây giờ bạn là giấc mơ của tôi ”. Tiếp theo, một hạt giống hoa được đặt vào chậu.
2. Sau nguyên tố Đất, câu thần chú mang năng lượng Nước.. Nghi thức này bao gồm việc tưới nước cho hạt giống, đi kèm với các từ "Nước và đất, hồi sinh những hạt giống ”. Như trong trường hợp trước, Ra tuyên bố 3 lần.
3. Tiếp theo đến lượt các yếu tố của Không khí. Nên đưa chậu cây tương lai ra cửa sổ mở và nói: "Bạn, Không khí, tôi cần, thích ánh sáng, và cho giấc mơ của tôi Bình minh ". Nó phải được lặp lại trong 3 ngày.
4. Khi một mầm hạt xuất hiện, đã đến lúc các nguyên tố của Lửa. Cần có một ngọn nến mới thắp sáng để đánh thức thần chú. Nó phải được đặt bên cạnh nhà máy và, tập trung, nói ba lần: "Nó đang cháy, Ngọn lửa, nến - cháy hết, và tiêu diệt nghèo đói. Để mầm lớn lên, tiền trốn cái gì. Và tôi sẽ thăng hoa cùng anh ấy, thu hút sự giàu có bằng tiền ".

Sau các bước này, mã tiền tệ bắt đầu hoạt động. Không nên vứt bỏ chậu có mầm và câu kỷ tử., tiếp tục chăm sóc cây thông thường.

ngoài ra, để nâng cao tác dụng của mã thần chú, bạn có thể áp dụng hình ảnh của các con số trên một tờ bìa cứng bằng cách sử dụng mực xanh và đỏ. Một lá bùa hộ mệnh tiền bạc như vậy phải thường xuyên mang theo bên mình..

Sự kỳ diệu của những điều quen thuộc

Trình tạo số ngẫu nhiên ngẫu nhiên của chúng tôi trực tuyến.

Trình tạo ngẫu nhiên của chúng tôi không yêu cầu tải nó xuống PC cá nhân của bạn. Mọi thứ xảy ra trong chế độ tạo số trực tuyến. Chỉ cần chỉ định các thông số này, như: dãy số trực tuyến, trong đó các số sẽ được chọn ngẫu nhiên. Cũng cho biết số lượng các số, cái nào sẽ được chọn.
Ví dụ, у Вас есть группа Вконтакте. В группе вы разыгрываете 5 giải thưởng, trong số những người tham gia, ai sẽ đăng lại bản ghi. Sử dụng một ứng dụng chuyên dụng, chúng tôi có một danh sách những người tham gia. Mỗi người đã được gán một số thứ tự cho các số trực tuyến.

Bây giờ, hãy truy cập trình tạo trực tuyến của chúng tôi và chỉ định phạm vi số (số lượng người tham gia). ví dụ, hỏi, những con số trực tuyến cần 5, kể từ khi chúng tôi có 5 giải thưởng. Теперь жмем кнопку генерации. Sau đó, chúng tôi nhận được 5 số ngẫu nhiên trực tuyến, từ 1 đến 112 bao gồm. Đã tạo 5 số trực tuyến sẽ tương ứng với số thứ tự của năm người tham gia, ai đã trở thành người chiến thắng trong bức vẽ. Mọi thứ thật đơn giản và tiện lợi.

Một điểm cộng khác của trình tạo số ngẫu nhiên là, rằng tất cả các số trực tuyến được đưa ra ngẫu nhiên. Đó là, để ảnh hưởng đến anh ta, hoặc tính toán, số nào sẽ là tiếp theo, dường như không thể. Những gì máy phát điện làm có thể nói, trung thực và đáng tin cậy, và chính quyền, xổ số giải thưởng bằng cách sử dụng trình tạo miễn phí của chúng tôi, trung thực và đàng hoàng khi đối mặt với những người tham gia cuộc thi. Và nếu bạn đang nghi ngờ về một giải pháp, thì bạn có thể sử dụng trình tạo câu trả lời có hoặc không của chúng tôi.

Cách tính mã tài sản của bạn

Có sự kết hợp tốt và xấu

Numerology và tiền có quan hệ mật thiết với nhau. Có các tổ hợp số, tạo ra của cải, nhưng có những sự kết hợp không thành công. Nếu bạn áp dụng chúng một cách chính xác, thành công và may mắn sẽ đứng về phía bạn. Tính toán mã rất dễ dàng. Để làm được điều này, bạn cần thực hiện các phép tính sau:

• viết số của bạn trên một mảnh giấy trắng, tháng và năm sinh (ví dụ, 31.10.1987);
• để tính toán giá trị thành công, hai chữ số đầu tiên nên được thêm vào, I E, ngày sinh cụ thể (ví dụ, 31 - 3 + 1 = 4). Số này sẽ là số đầu tiên trong tổ hợp;
• để tính toán ký tự thứ hai của kết hợp, nó là cần thiết để tính toán giá trị của tháng (ví dụ, Tháng Mười, 10 tháng - 1 + 0 = 1);
• bây giờ bạn cần phải tính toán số tiền của năm sinh (ví dụ, 1987 - 1 + 9 + 8 + 7 = 25, 2+5= 7);
• cuối cùng, bạn cần tính toán cá nhân ký tự cuối cùng của tổ hợp, đối với điều này, tất cả ba số đã nhận trước đó được cộng lại (ví dụ, 4+1+7= 12, 1+2= 3, trong trường hợp này, kết hợp tiền là 4173). Kết quả kết hợp là một mã cá nhân cho một người..

Ngoài mã cá nhân, có những giá trị phổ quát, mà mọi người có thể áp dụng, như một triệu phú, và với thu nhập trung bình. Đây là một linh vật kỹ thuật số, được mô tả dưới dạng bốn phần tám có kích thước bằng nhau. Sự kết hợp này rất mạnh mẽ, có nghĩa là tiền tệ thành công và ổn định.

Bạn cũng có thể tính toán sau đó, Tôi sẽ giàu không, bằng tên. Đối với điều này, một bảng tương ứng giữa các chữ cái và số được lấy. Ví dụ, Bến du thuyền, được sinh ra 5 con số. Trong trường hợp này, chỉ lấy ngày sinh:

M-5, A-1, R-9, I-1, N-6, A-1. 5+1+9+1+6+1= 23, 2+3= 5. Tiếp theo, thêm ngày sinh - 5 + 5 = 10, 1+0= 1 - một và là mã may mắn và tiền bạc cho một người cụ thể. Nhưng liệu anh ấy có thể thành công, phụ thuộc, nó được sử dụng tốt như thế nào.

Hoán vị của n phần tử

Định nghĩa 3. Hoán vị
trong số n phần tử
bất kỳ bộ có thứ tự nào được gọi là
những yếu tố này.

Ví dụ 7a. Tất cả các loại hoán vị
nhiều, bao gồm ba yếu tố {1, 2, 3} Chúng tôi: (1, 2, 3), (1, 3,
2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

Số hoán vị phân biệt của n phần tử được ký hiệu là P_n và
được tính bằng công thức P_n= n!.

Thí dụ 8. Trong bao nhiêu cách bảy cuốn sách
các tác giả khác nhau có thể được sắp xếp thành một hàng trên giá?Phán quyết:vấn đề này về số
sắp xếp lại bảy cuốn sách khác nhau. Có P₇= 7!= 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040
cách sắp xếp sách.

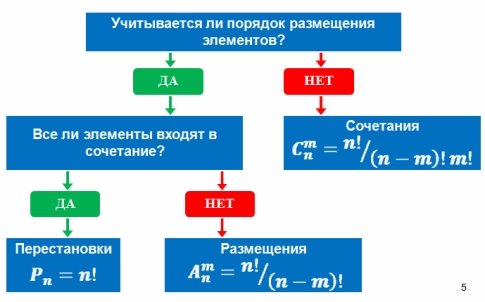
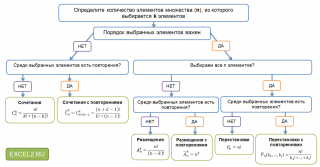
Thảo luận. Chúng tôi thấy,
rằng số lượng các kết hợp có thể có có thể được tính toán theo các quy tắc khác nhau
(hoán vị, sự kết hợp, vị trí) và kết quả sẽ khác,
bởi vì. nguyên tắc đếm và bản thân các công thức khác nhau. Nhìn kỹ vào
các định nghĩa, có thể được nhìn thấy, rằng kết quả phụ thuộc vào một số yếu tố
đồng thời.
Lúc đầu, từ đó, từ bao nhiêu phần tử chúng ta có thể kết hợp chúng
bộ (tổng số nguyên tố lớn bao nhiêu).
Thứ hai, kết quả phụ thuộc vào, tập hợp các phần tử đối với chúng ta lớn như thế nào
nhu cầu

Và cuối cùng, điều quan trọng là phải biết, là dành cho chúng tôi
thứ tự thiết yếu của các mục trong một bộ. Hãy để chúng tôi giải thích yếu tố cuối cùng về
ví dụ sau

Thí dụ 9. Tại cuộc họp phụ huynh
hiện tại 20 Đàn ông. Có bao nhiêu tùy chọn thành phần khác nhau
ban phụ huynh, nếu nó nên nhập 5 Đàn ông?Phán quyết: Trong ví dụ này, chúng tôi
không quan tâm đến thứ tự tên trong danh sách ủy ban. Kết quả là nếu trong
thành phần sẽ là những người giống nhau, thì ý nghĩa đối với chúng ta là như nhau
Lựa chọn. Do đó, chúng ta có thể sử dụng công thức để tính số lượng kết hợp từ 20 các yếu tố của 5.
Mọi thứ sẽ khác, nếu mỗi thành viên ban đầu chịu trách nhiệm về
phương hướng làm việc xác định. Sau đó, với cùng một bảng lương
ủy ban, bên trong nó có thể 5! các tùy chọn hoán vị, vấn đề nào. con số
khác nhau (và thành phần, và theo lĩnh vực trách nhiệm) các tùy chọn được xác định trong
trong trường hợp này, số lượng vị trí
của 20 các yếu tố của 5.

Nhiệm vụ tự kiểm tra
1. Từ các chữ số có thể lập được bao nhiêu số chẵn có ba chữ số 0, 1, 2, 3, 4, 5,
6, nếu các con số có thể được lặp lại?
Từ. một số chẵn ở vị trí thứ ba có thể là 0, 2, 4, 6, I E. Bốn con số. Bất kỳ chữ số nào trong số bảy chữ số đều có thể ở vị trí thứ hai. Bất kỳ chữ số nào trong số bảy chữ số khác 0 đều có thể ở vị trí đầu tiên, I E. 6 những cơ hội. Kết quả = 4 * 7 * 6 = 168.
2. Có bao nhiêu số có năm chữ số, đọc giống nhau ở bên trái
phải và phải sang trái?
Bất kỳ số nào cũng có thể ở vị trí đầu tiên ngoại trừ 0, I E. 9 những cơ hội. Bất kỳ số nào cũng có thể đứng ở vị trí thứ hai, I E. 10 những cơ hội. Bất kỳ số nào từ, I E. 10 những cơ hội. Các chữ số thứ tư và thứ năm được xác định trước, họ phù hợp với thứ nhất và thứ hai, vì thế, số các số đó là 9 * 10 * 10 = 900.
3. Có mười môn học và năm bài học mỗi ngày trong lớp. Bằng nhiều cách bạn có thể
lên lịch cho một ngày?
4. Bạn có thể chọn bao nhiêu cách 4 ủy nhiệm cho hội nghị, nếu trong một nhóm
20 Đàn ông?

n = C₂₀4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)= 4845.

5. Có bao nhiêu cách có thể chia tám chữ cái khác nhau thành tám chữ cái
phong bì khác nhau, nếu chỉ có một lá thư được bỏ vào mỗi phong bì?
Bạn có thể cho vào phong bì đầu tiên 1 trong số tám chữ cái, ở cái thứ hai trong số bảy cái còn lại, trong một phần ba một trong sáu v.v.. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Ba nhà toán học và mười nhà kinh tế học phải bao gồm một ủy ban,
bao gồm hai nhà toán học và sáu nhà kinh tế. Có bao nhiêu cách là nó
có thể được thực hiện?

Số cách chọn toán C₃2= 3!/(2!*(3-2))!= 3/2, số cách chọn nhà kinh tế học C₁₀6= 10!/(6!*(10-6))!= 7 * 8 * 9 * 10 /(1*2*3*4)= 210. n = C₃2*TỪ₁₀6= 3 * 210 = 630.