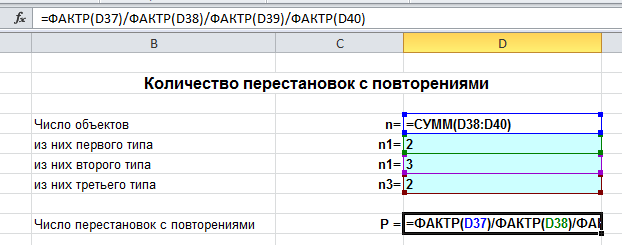
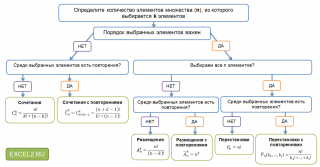
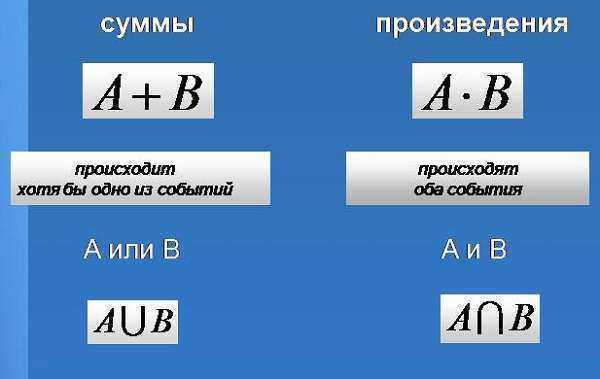
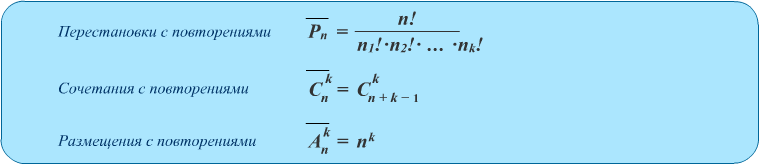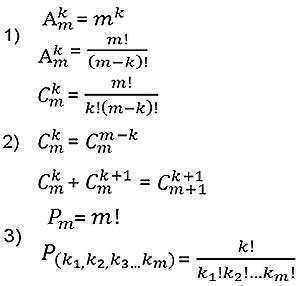组合学, 基本组合公式

内容

命理学中的金钱魔术

每个数字都有自己的能量，并以某种方式影响一个人的生活。. 货币命理有助于确定数字的含义, 找出金钱和财富的个人守则. 财政代码是使用出生日期计算的. 那你需要看成绩单. 您还需要知道, 如何正确使用您的财富代码.

最主要的是正确计算财务代码

除了, 多少钱, 也有数字, 没有丰富一个人的生活. 需要避免. 吸引资金流, 需要熟悉一下, 每个数字代表什么:

零一. 命理学家相信, 这些数字和代码对货币能量不利, 他们不会带来好运. 因此，您应该避免节省。, 有金额的存款, 这些数字存在, 因为它们会减慢现金流并且不会带来繁荣和成功.
一对. 这是一个不开心的数字. 她不会带来繁荣和成功. 不建议使用这种面额的钞票进行节省。, 不要把它们放在钱包里.
三人组. 财务上有利, 借助它，一个人可以中奖, 寻找其他收入来源. 但是，命理学家不建议积累资金。, 总和是 300, 3000, 30000. 这个数字需要不断的运动, 她需要能量, 不和平. 最好的办法是以这样的金额购买彩票或将其投资于自己的业务。.
个人密码中的四个是稳定的象征, 可靠性. 节省的理想选择, 储蓄, 投资是票据的金额 400, 4000, 40000. 通过这种方式, 财富会增加.
五是命理学中非常重要的财富数字代码. 有这个数字的钞票是真钱的磁铁。. 他们可以借, 花在旅行上, 积累, 花那么多, 随你便.
这样的财务代码可能涉及某些财务约束。. 有了这个数字，人们学会了保存, 控制您的支出. 金额 600, 6000 是稳定和确定性的象征. 命理学家不建议投资这样的金额.
七是代码, 厄运, 它不能用于存储, 投资额, 储蓄, 贷款和任何其他金融交易, 与风险相关的.
八是命理学上的强大财富法则, 他被认为非常成功. 存款金额 800, 8000, 80000 非常成功, 他们吸引金钱, 像一块磁铁.
九是精神和内在发展的象征. 用它筹集资金不会发生, 但也不会有损失. 建议在自学上花费9分之和, 训练

正确使用数字, 需要知道, 如何计算财富代码. 接下来，您需要找出使用这种组合的规则。. 我会致富吗, 不仅取决于计算所得的代码, 而且从那, 如何正确使用.

参考信息

文件资料报告书提及单据证券规定财务文件决议案按主题的专栏按确切日期的俄罗斯联邦区域城市条款科学术语金融经济时间日期2015 2016投资中金融部门的文件

赢得世界上最大的大奖是真实的!!! 尝试! →

组合无重复

一个任务: 查找所有可能的组合，而无需重复许多元素 {1,2,3} 通过 2.
存在以下组合:1: 1 22: 1 33: 2 3
不重复M的N个元素的可能组合数可以由下式确定 (N≥M):

在M中! 倍于相应的展示位置数量（无重复） (因为没有重复的组合不取决于元素的顺序).
考虑通过M获得数字1 ... N的所有组合的问题。用C ++实现

12345678910111213141516171819202122232425262728293031323334353637383940414243

#包括 <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int k = m; 对于 (int i = k – 1; 一世 >= 0; –一世) 如果 (一种 < ñ – ķ + 一世 + 1) { ++一种; 对于 (int j = i + 1; j < ķ; ++j) a = a + 1; return true; } 返回假;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; 对于 (int i = 0; 一世 < ñ; i++) cout << 一种 << ” “; cout << endl;}int main() { int n, 米, *一种; cout << “N = “; cin >> ñ; cout << “M = “; cin >> 米; a = new int; 对于 (int i = 0; 一世 < ñ; i++) a = i + 1; Print(一种, 米); 如果 (ñ >= m) { 而 (下一集(一种, ñ, 米)) Print(一种, 米); } cin.get(); cin.get(); 返回 0;}

Результат выполнения

英语命理学: 概念与本质

最古老的知识, 这有助于解释, 解释, 天使想告诉男人什么, 称为天使命理学.

召回, 命理学研究数字振动, 数字, 他们对人及其生活过程的影响. 另一位英语数学家, 占星学家约翰·迪（John Dee）在16世纪撰写了有关数字的著作, 他认为这是与人交流的通用天使语言.

最可靠的中介，可以用来打外国彩票 18 年-世界彩票的主要在线超级市场! 赢得世界各地最好的彩票! →

相对较年轻的天使命理学教学的创始人是多琳·维尔切（Doreen Verche）. 来自美国的千里眼, 心理学家和哲学家, 许多书的作者. 她将自己的作品奉献给至尊生物, 包括神, 天使, 圣人. 多年来，她一直在研究无法解释的现象。. 但它是值得的. 她创造了乐器, 谁可以帮助您解释来自天堂的助手的信息. 根据Doreen Verce的说法, 我们会定期收到天使的信号, 警告危险, 为人的生活中的问题提出解决方案.

天使通过数字与人交谈, 字母, 迹象. Doreen Verce的作品谈论了隐形饲养员的线索, 以重复数字或其组合编码的. 即:

在汽车牌照上;
在时钟上;
在布朗尼蛋糕, 公寓, 办公室编号;
在出生日期;
机票形式, 喜欢在运输中, 和公共设施等.

在所有这些组合中, 数字隐藏数据, 谁可以调整人们的未来. Doreen Verce已经对该主题进行了大量研究, 致力于按出生日期进行命理计算. 这样的计算有助于识别孩子。, 从出生起就有独特能力, 不仅.

号码匹配, 我们通常不会注意到的组合

但是值得关注, 因为这种现象可能是重要的警告. 毕竟，天使没有为我们送出这样的标志

结合重复

重复的组合称为M元素集, 其中集合N的每个元素可以参与多次. 在这种情况下，对M和N的值的比例没有限制, 与重复的组合总数为

此类问题的一个示例是，以所有可能的方式从N个中选择M张明信片.

要生成具有重复的组合，我们将使用该解决方案生成具有重复的展示位置, 考虑过的C ++实现

仅在线验证外国彩票! 成为流行游戏的赢家! →

1234567891011121314151617181920212223242526272829303132333435363738394041

#包括 <iostream>using namespace std;bool NextSet(int *a, int n, int m){ int j = m – 1; 而 (a == n && j >= 0) j–; 如果 (j < 0) 返回假; 如果 (一种 >= n) j–; a++; 如果 (j == m – 1) return true; 对于 (int k = j + 1; ķ < 米; k++) a = a; return true;}void Print(int *a, int n) { static int num = 1; cout.width(3); cout << num++ << “: “; 对于 (int i = 0; 一世 < ñ; i++) cout << 一种 << ” “; cout << endl;}int main() { int n, 米, *一种; cout << “N = “; cin >> ñ; cout << “M = “; cin >> 米; int h = n > 米 ? ñ : 米; // размер массива а выбирается как max(ñ,米) a = new int; 对于 (int i = 0; 一世 < H; i++) a = 1; Print(一种, 米); 而 (下一集(一种, ñ, 米)) Print(一种, 米); cin.get(); cin.get(); 返回 0;}

以上算法的结果:

算法化

组合学的基本公式

设k组元素, 第i个组由n个组成_一世元素.
从每个组中选择一个元素. 然后总数N,
可以做出这样的选择, 由关系N = n定义₁*ñ₂*ñ₃*…*ñ_ķ.

例 1. 让我们简单地解释一下这个规则
例. 让有两组元素, 第一组包括
ñ₁ 元素, 第二个 – 的n₂ 元素. 多少
两组不同的元素可以组成, 通过这种方式,
这样每个组中成对存在一个元素? 让我们承认, 我们拿了
第一组的第一个元素和, 不改变它, 超越了一切可能
情侣, 仅更改第二组中的元素. 这种元素的配对
可以是n₂. 然后我们从第一组中取出第二个
并为此组合所有可能的对. 也将有n个这样的对₂.
由于第一组仅包含n₁ 元件, 可能的
选项将为n₁*ñ₂.例 2. 多少
三位偶数可以由数字组成 0, 1, 2, 3, 4, 5, 6, 如果
数字可以重复?决断: ñ₁= 6
(因为. 作为第一个数字，您可以从 1, 2, 3, 4, 5, 6), ñ₂= 7
(因为. 作为第二个数字，您可以从 0, 1, 2, 3, 4, 5,
6), ñ₃= 4 (因为. 作为第三个数字，您可以从 0, 2, 4,
6).

所以, N = n₁*ñ₂*ñ₃= 6 * 7 * 4 = 168.

在这种情况下, 当所有组具有相同数量的元素时, 即. ñ₁= n₂=…ñ_ķ= n
可以考虑, 每个选择都是来自同一组, 此外
选择后的元素再次返回到组. 然后所有方式的数量
选择是nk. 组合学中的这种选择类型称为带有收益的选择.

例 3. 四位数是多少
可以由数字组成 1, 5, 6, 7, 8?决断. 对于每个等级
一个四位数的数字有五种可能性, 表示N = 5 * 5 * 5 * 5 = 54 = 625.

考虑集合, 由n个元素组成. 它
组合中的一个集合称为通用
骨料.

世界上最大的JACKPOT正在等待您! 多于 100 000$!!! →

商业与金融

银行财富与福利腐败(犯罪)营销管理投资证券管理公共股份公司项目文件证券 – 控制证券 – 估值债券债务货币房地产(出租)专业职位招聘交易服务金融保险预算服务金融服务

完成仪式后如何处理Mantric代码

后, 在期间如何读取数值 77 天, 他们应该被起诉 4 进一步工作的要素.

为此，您需要执行简单的操作。:

利用地球的能量激活代码. 一小盆土适合该仪式。. 您还将需要任何花种子. 这些应该正是种子。, 不是植物的芽和块茎. 准备好所需属性后, 咒语应该写在一张白纸上，埋在地下, 说了三遍：“地球上到处都是财富, 你现在是我的梦想”. 接下来，将花种子放入花盆中.
在地球元素之后，咒语充满了水的能量. 这个仪式包括给种子浇水, 伴随着“水与土, 复兴种子”. 和以前一样, 发表声明 3 次.
接下来是空气元素的转变. 装有未来植物的花盆应打开窗户，并说: “您, 空气, 我需要, 像光, 给我梦想的黎明. 必须在 3 天.
当种子发芽时, 该是火元素的时候了. 需要新点燃的蜡烛才能唤醒咒语. 必须将其放置在工厂旁边，并且, 专心, 说三遍: “它在燃烧, 火, 蜡烛-烧光, 消灭贫穷. 让新芽生长, 钱藏了什么. 我会和他一起繁荣, 吸引财富”.

这些步骤之后，货币代码开始工作. 建议不要将芽菜和咒语扔掉。, 继续对植物进行日常护理.

除了, 增强Mantric代码的效果, 您可以使用绿色和红色墨水在纸板上应用数字图像. 这样的金钱护身符必须经常随身携带。.

熟悉事物的魔力

我们的在线随机数发生器.

我们的随机发生器生成器不需要将其下载到您的个人PC. 一切都在在线号码生成器模式下发生. 只需指定这些参数, 如: 在线数字范围, 其中将随机选择数字. 同时标明数字, 将被选择.
例如, у Вас есть группа Вконтакте. В группе вы разыгрываете 5 奖品, 在参与者中, 谁将重新发布记录. 使用专用应用, 我们有参与者名单. 每个号码均已分配一个在线号码的序号.

现在转到我们的在线生成器并指定数字范围 (参加人数). 例如, 问, 在线需要什么数字 5, 因为我们有 5 奖品. Теперь жмем кнопку генерации. 然后我们得到 5 在线随机数, 从 1 至 112 包括的. 产生的 5 在线号码将对应于五个参与者的序列号, 谁成为图纸的赢家. 一切都很简单方便.

随机数生成器的另一个优点是, 在线上的所有数字都是随机分配的. 那就是要影响他, 或计算, 下一个数字是多少, 似乎不可能. 发电机的作用可以说, 诚实可靠, 和政府, 使用我们的免费生成器赠送奖品, 在比赛参赛者面前诚实诚实. 如果您对解决方案有疑问, 那么您可以使用我们的是或否答案生成器.

如何计算您的财富代码

有好有坏组合

命理学与金钱息息相关. 有数字组合, 创造财富, 但组合失败. 如果正确应用它们, 成功和运气将在您身边. 计算代码很容易. 为此，您需要执行以下计算:

将您的电话号码写在一张空白的纸上, 出生月份和年份 (例如, 31.10.1987);
计算成功值, 前两位应加, 即, 具体的出生日期 (例如, 31 – 3 + 1 = 4). 该号码将是组合中的第一个;
计算组合的第二个字符, 有必要计算月份的值 (例如, 十月, 10 月-1 + 0 = 1);
现在您需要计算出生年份 (例如, 1987 – 1 + 9 + 8 + 7 = 25, 2+5= 7);
最后，您需要亲自计算组合的最后一个字符, 为此，将之前收到的所有三个数字相加 (例如, 4+1+7= 12, 1+2= 3, 在这种情况下，货币组合为 4173). 结果组合是一个人的个人密码。.

除了个人密码, 有普世价值, 每个人都可以申请, 像百万富翁, 中等收入. 这是一个数字吉祥物, 以相等大小的四分之八的形式表示. 这个组合很强, 意味着金钱上的成功和稳定.

您还可以计算, 我会富有吗, 按名字. 为此，采用字母和数字之间的对应表. 例如, 码头, 哪个出生 5 数字. 在这种情况下，只有生日:

M-5, A-1, R-9, I-1, N-6, A-1. 5+1+9+1+6+1= 23, 2+3= 5. 接下来，添加出生日期-5 + 5 = 10, 1+0= 1-一个，是特定人的运气和金钱代码. 但是他能成功吗, 取决于, 使用得如何.

n个元素的排列

定义 3. 排列
的n个元素
任何有序集都称为
这些要素.

实施例7a. 各种排列
众多的, 由三个要素组成 {1, 2, 3} 是: (1, 2, 3), (1, 3,
2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

n个元素的不同排列数由P表示_ñ 和
由公式P计算_ñ= n!.

例 8. 用多少种方式七本书
可以将不同的作者排成一排在书架上?决断:这个数字的问题
重新整理七本不同的书. 有P₇= 7!= 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040
整理书籍的方法.

讨论区. 我们看,
可以根据不同的规则计算出可能的组合数量
(排列, 组合, 放置) 结果会有所不同,
因为. 计数原理和公式本身是不同的. 仔细看
定义, 看得见, 结果取决于几个因素
与此同时.
首先, 从那个, 我们可以从几个元素中组合它们
套 (元素总数是多少).
其次, 结果取决于, 对我们来说元素集有多大
需要

最后, 重要的是要知道, 是给我们的
一组项目的基本顺序. 让我们解释一下
下面的例子

例 9. 在家长会上
当下 20 人. 有多少种不同的构图选项
上级委员会, 是否应该输入 5 人?决断: 在这个例子中，我们
对委员会名单上的姓名顺序不感兴趣. 结果，如果
组成将是同一个人, 那么对我们来说意义是一样的
选项. 因此，我们可以使用公式来计算 20 元素由 5.
情况会有所不同, 如果每个委员会成员最初负责
明确的工作方向. 然后用相同的工资单
委员会, 里面是可能的 5! 排列选项, 哪件事. 数
不同 (和组成, 以及责任领域) 在中定义的选项
在这种情况下，展示位置的数量
的 20 元素由 5.

自检任务
1. 一个数字可以形成多少个三位数的偶数 0, 1, 2, 3, 4, 5,
6, 如果数字可以重复?
以来. 第三位的偶数可以是 0, 2, 4, 6, 即. 四位数. 七个数字中的任何一个都可以排在第二位. 首先可以是除零以外的七个数字中的任何一个, 即. 6 机会. 结果= 4 * 7 * 6 = 168.
2. 有多少个五位数, 左边写的一样
从右到右?
任何数字都可以放在首位，除了 0, 即. 9 机会. 任何数字都可以排第二, 即. 10 机会. 来自的任何数字, 即. 10 机会. 第四和第五位数字是预定义的, 他们匹配第一和第二, 因此, 这样的数字的数量是9 * 10 * 10 = 900.
3. 每天有十门科目和五堂课. 您可以通过许多方式
安排一天的行程?
4. 您可以选择多少种方式 4 代表参加会议, 如果在一个小组中
20 人?

n = C₂₀4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)= 4845.

5. 八个不同的字母可以通过几种方式分解为八个
各种信封, 如果每个信封只放一个字母?
你可以放第一个信封 1 八个字母, 在剩下的七个中的第二个中, 在六个中的第三个中等等. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. 必须由一个委员会组成三名数学家和十名经济学家,
由两位数学家和六位经济学家组成. 有多少种方法
可以做到?